你也可以在自己的Linux kernel 源码目录执行以下命令生成自己的pdf,但何必自己造轮子呢。
sudo apt-get install sphinxsearch
sudo apt-get install python-sphinx-rtd-theme
sudo apt-get install texlive-latex-recommended
sudo apt-get install texlive-base
sudo apt-get install graphviz
sudo apt-get install imagemagick
/usr/bin/virtualenv ~/sphinx_version
. ~/sphinx_version/bin/activate
pip install -r Documentation/sphinx/requirements.txt
make pdfdocs分类目录归档:其他
寻找最大容错的扁平XOR 码
参考:
[1] Finding the most fault-tolerant flat XOR-based erasure codes for storage systems [PDF]
[2] Determining fault tolerance of XOR-based erasure codes efficiently [PDF]
本文内容主要来源于上面两篇文章,主要讨论暴力搜寻方法具有最大容错能力(most fault-tolerant)的扁平(Flat)XOR 码。
XOR 码是通过异或运算(exclusive OR)进行数据编码、解码和重建的编码方法,其生成矩阵可以用1/0 二进制矩阵表示。
扁平码是一种每个节点只保存一个符号(数据块),即生成矩阵的每一行(列)对应一个节点。k 和m 分别表示原始数据块个数和校验块个数的话,扁平码的生成矩阵是一个(k+m)×k 大小的0/1 矩阵。常见的RS 码是扁平码,但不是XOR 码;CRS 码不是扁平码,是XOR 码。
暴力搜索通过遍历所有的解空间(所有可能的(k, m) 编码),通过计算每个解的性质,找到满足条件的编码。一个(k+m)×k 大小的0/1 矩阵有2^((m+k)×k) 种可能的二进制矩阵,如果将编码限制在系统码中,则有2^(m×k) 种可能的二进制矩阵。
[2] 中介绍了一种ME (Minimal Erasures)算法,是暴力搜索的关键,该算法通过找到最小失效列表(Minimal Erasure List)寻找某种编码的最大容错能力。ME 算法会用到几个术语:
汉明距离(Hamming distance):如果一个编码的汉明矩阵是d,那么它能容忍的最大失效节点少于d 个。
失效样式(Erasure pattern):一组失效(的数据块)使得有一个原始数据块无法被恢复。
失效列表(Erasure list):所有失效样式的集合。
失效矢量(Erasure vector):长度为m 的矢量,其中第i 个元素是失效列表中长度为i 的失效样式个数的总和。比如 < 0, 0, 3, 7, …> 表示有失效列表中有3 个长度为3 的失效样式,有7 个长度为4 的失效样式。失效矢量中第d 个值是第一个非零值(小于d 的失效均可恢复)。
最小失效(Minimal Erasure,ME)是一种特殊的失效样式,它的每个失效元素都是必须的,如果去掉其中之一,它就不再是失效样式。
最小失效列表(Minimal Erausre List,MEL)是一个编码的所有最小失效的集合。
最小失效矢量(Minimal Erasure Vector,MEV)是一个长度为m 的矢量,其第i 个元素是MEL 中长度为i 的ME 的个数。
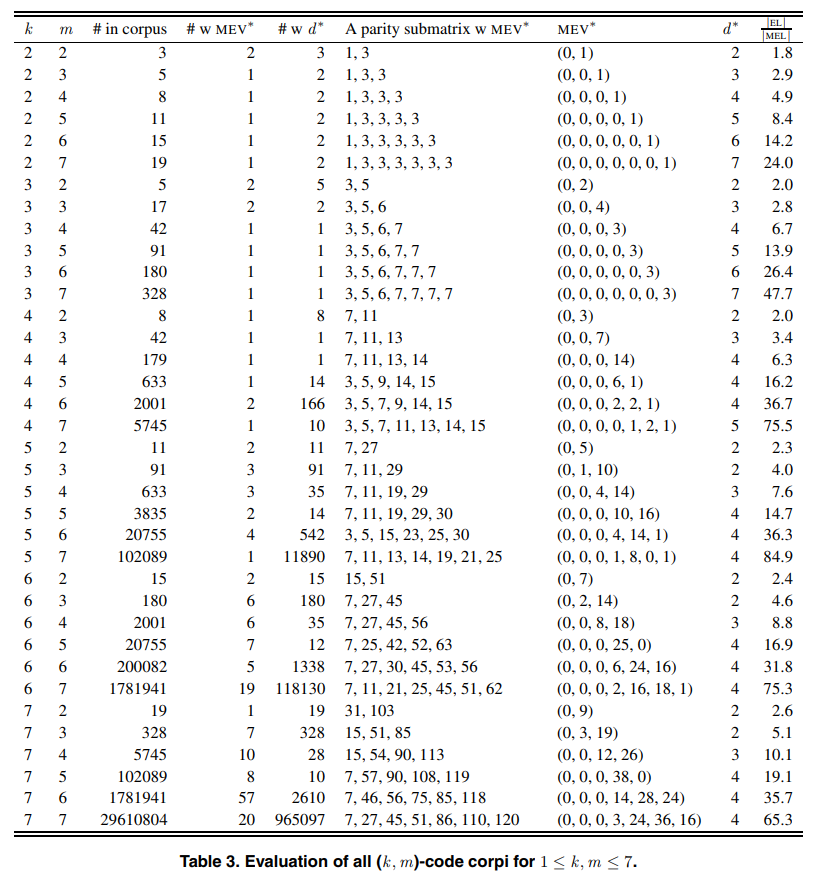
ME 算法具体详见[2] ,其输入是编码的生成矩阵(或Tanner 图),输出为MEL 和MEV。下图给出了 m < 8 和 k < 8 的结果。
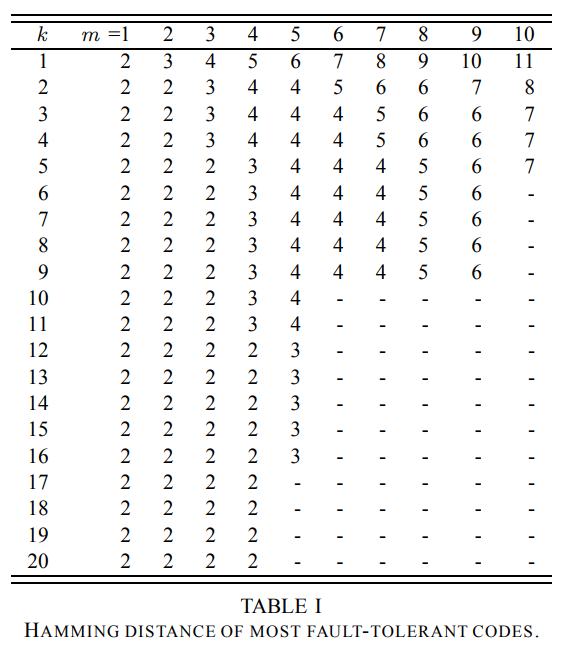
下图是m < 11 和 k < 21 所有扁平XOR 码的最大汉明距离。
下图是m < 11 和 k < 21 所有扁平XOR 码中具有最优容错的个数。
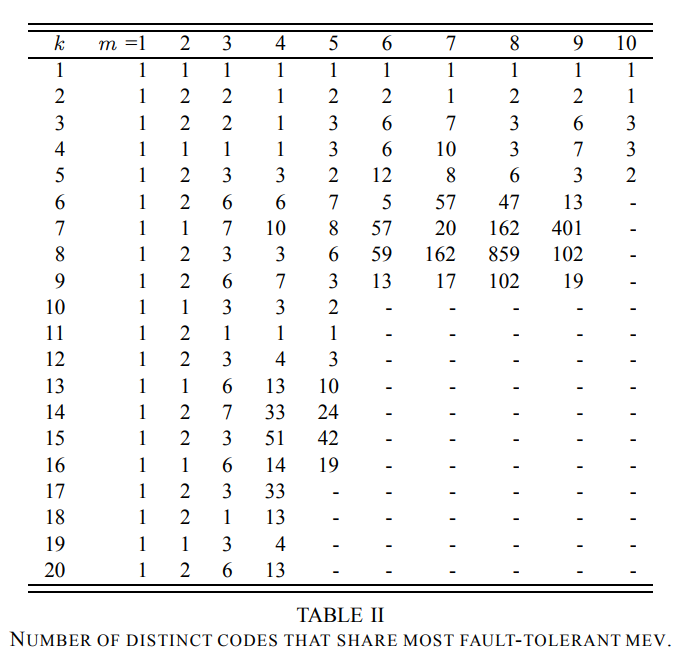
下图是下图是m < 11 和 k < 21 所有扁平XOR 码中能够达到最大汉明距离的个数。
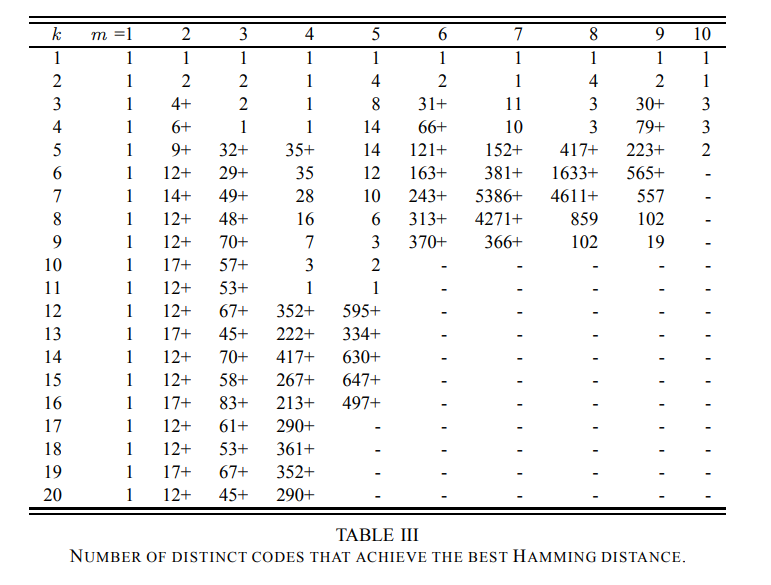
[1] 还介绍了如何减少搜索的解空间等优化的方法,并指出搜索算法有部分是Python 写的,用C 能够进一步提高运算速度,并增加m 和k 的值。
遗传算法解决数学等式(续)
之前的文章(http://blog.foool.net/2017/08/用遗传算法解决简单的数学等式问题/) 中介绍了过如何使用遗传算法解决数学等式问题,即寻找满足等式
(a + 2b + 3c + 4d) – 30 = 0
的一组解。适应函数确定后,影响算法好坏的主要依赖于交叉概率(crossover ratio),变异概率(mutation ratio)、初始基因组大小(即用于交叉变异的基因个数)和基因初始阈值。基因初始阈值指的是基因的取值范围,比如等式中变量a/b/c/d 的取值范围,我在实验中限定变量为大小不超过100 的整数。下面给出本文的几个结论。
一、遗传算法也可以用于寻找唯一解
之前的文章 中寻找的是四元一次等式的一个解,这个解的个数是无穷的,遗传算法能够找到一个解,但每次找到的解也不相同。但如果要用遗传算法解一个包含四个等式的四元一次方程组(唯一解)也是可行的,只是时间话的需要更长。比如遗传算法解四元一次等式平均需294 次迭代,解四元一次方程组需11400 次迭代(所有参数同之前的文章)。本文使用的四元一次方程组为:
(a + 2b + 3c + 4d) – 30 = 0
(2a + 2b + 2c + 2d) – 24 = 0
(3a + 1b + 7c + 1d) – 60 = 0
(4a + 3b + 2c + 1d) – 30 = 0
二、增加初始基因组大小有可能加速算法速度
增加基因组中基因数量,那么每次迭代/循环中的基因数量更多,可能出现解的概率增大。在以四元一次等式为例的实验中,增加基因组大小的确显著减少了迭代的次数,即使考虑了增加基因数目而带来的增量计算,算法仍减少了程序的整体运行时间。
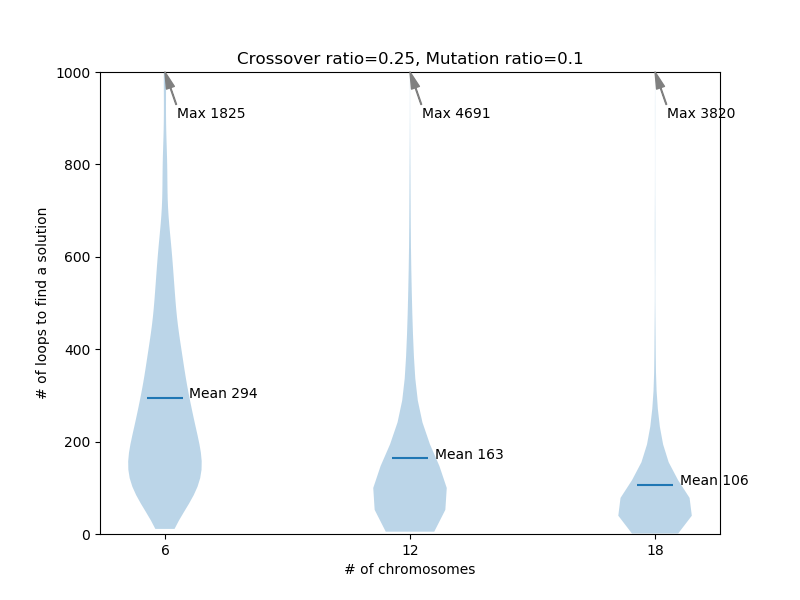
三、增加初始基因组大小也有可能不能加速算法速度
有点调皮了,这个结论是和第二点结论是相左的,如在其他参数相同情况下,随着基因组大小增大,遗传算法在解四元一次方程组需要迭代的次数增加。
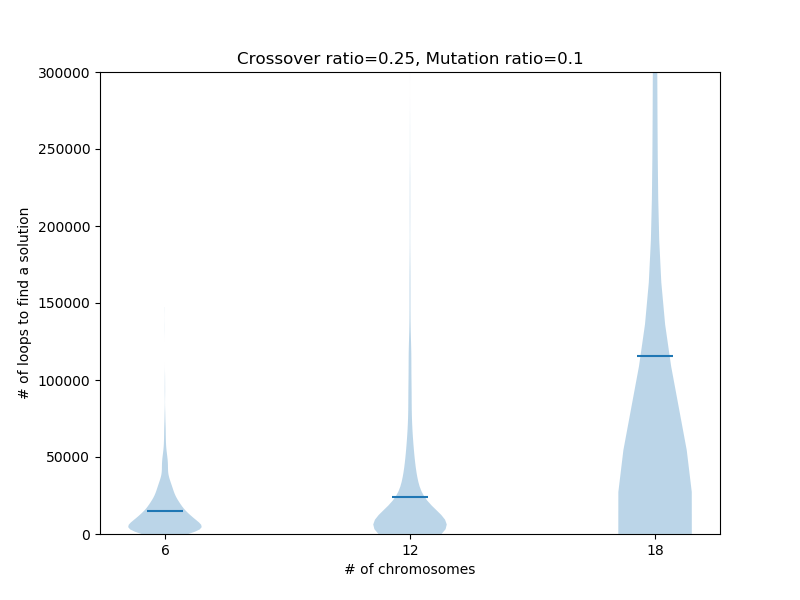
四、对于特定问题,参数大小影响算法性能大
下图是在基因组大小为18 时, 遗传算法1000 次测试四元一次等式求解所需要迭代次数的热力图,横坐标是变异率,从5% 到43%,纵坐标是交叉率,从5% 到70% 。热力图颜色范围是0-300,最深颜色表示300 次或300次以上迭代(比如在交叉率是70%,变异率是43%,实际迭代次数是9268次)。
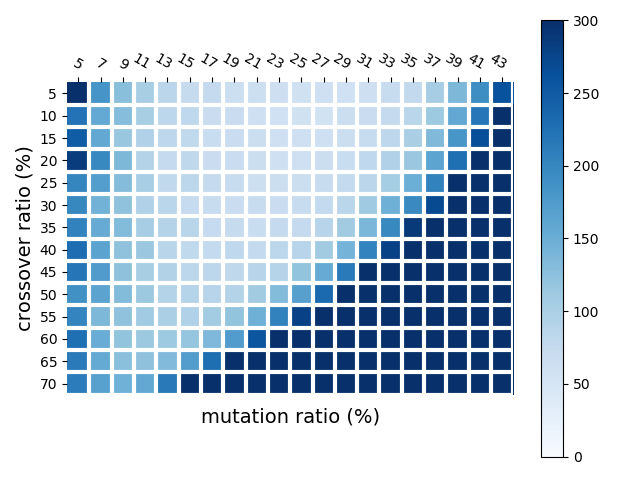
综上,1.借助于适应函数,交叉、变异过程,遗传算法给出了一个在较大解空间快速求解的途径,但具体设计交叉、变异过程需要考虑特定问题;2.选取合适的参数极大影响了遗传算法性能,一般可以通过相似问题(复杂度更低)的参数选择作为参考(但是这种参考也不一定可靠,比如上面例子中,四元一次方程中增大基因组个数可以减少迭代次数,但在四元方程组中增加基因组个数却增加了迭代次数)。
自循环字符串/周期性字符串的判别和概率
问题来源:需要判断一个长度为N 的0/1 二进制字符串是自循环的概率是多少?自循环指的是一个字符串循环移位s 位仍然可以得到其本身,s 小于字符串长度。比如,010010 是自循环的,因为将这个字符串循环右移三个bits 字符串还是其本身。
通过自循环字符串特征很容易推导出:自循环字符串是周期性字符串,即字符串完全由若干个相同子串拼接得到,上面例子中重复的子串是 010。并且,自循环字符串移位得到其本身需要的最少步数s 和最小子串长度相同,也就是说,计算得到字符串最小重复子串也就得到了其自循环需要移位数s。
那么问题归结为如何找到一个周期性字符串的最小重复子串?
算法:令周期性字符串为S,那么SS 是两个S 的拼接,从SS 第二个字符开始,利用字符串匹配寻找S,如果SS 从第c 个字符开始包含了S 字符串,则S 的最小周期子串长度为c。下面是两个例子:
例子一:S = 010010
SS = 010010010010
- 0 1 0 0 1 0 0 1 0 0 1 0 不是S
- 0 1 0 0 1 0 0 1 0 0 1 0 不是S
- 0 1 0 0 1 0 0 1 0 0 1 0 是S
结束,最小子串长度为3,即010 。
例子二:S = abaaabaaabaa
SS = abaaabaaabaaabaaabaaabaa
- a b a a a b a a a b a a a b a a a b a a a b a a
- a b a a a b a a a b a a a b a a a b a a a b a a
- a b a a a b a a a b a a a b a a a b a a a b a a
- a b a a a b a a a b a a a b a a a b a a a b a a
结束,最小子串长度为4,即abaa 。
接着统计了下二进制字符长度(X轴)和周期性字符串个数/概率(Y轴)关系。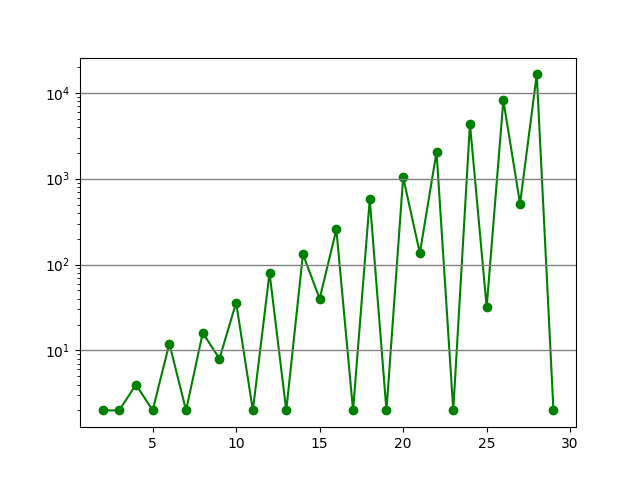
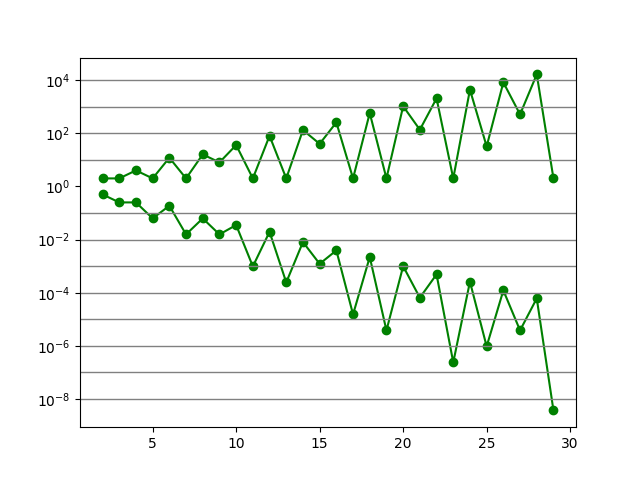
可见,自循环字符串个数和概率与其字符串长度有关,总的来说:
- 长度越长,包含的自循环的字符串个数越多,呈指数增加
- 长度越长,字符串可能是自循环的概率降低,呈指数下降
- 素数只有两个自循环字符串(全0,全1)
- 包含分解因子越多,越可能包含更多自循环字符串
用遗传算法解决简单的数学等式问题
[翻译]原文:Genetic Algorithm for Solving Simple Mathematical Equality Problem
[翻译]地址:https://arxiv.org/ftp/arxiv/papers/1308/1308.4675.pdf
[翻译]目的:文章旨在为新手解释什么是遗传算法。并使用遗传算法这个工具一步步解决一个具体的数学问题——求解数学等式的解。
基本理念
在通过遗传算法寻找问题解的过程中,用染色体来表示一个解,一堆染色体叫做种群。染色体由基因构成,基因可以是数值的、符号的也可以是其他类型数据结构(视所解决的问题来定)。染色体通过环境适应度来衡量这个解对于问题的优劣程度。种群中的染色体通过交叉(交配)遗传到下一代,子代染色体是父代基因的组合。基因还会发生突变,遗传算法中使用交叉率和突变率来控制。
算法步骤
- 决定染色体数目、循环代数(决定遗传多少代)、突变率和交叉率;
- 产生染色体种群,并使用随机值初始化染色体中的基因
- 重复步骤4-8(重复次数等于循环代数)
- 考量每个染色体的适应值
- 染色体选取
- 交叉
- 变异
- 产生新的后代染色体
- 得到最终解
算术问题
以求解多元一次不等式 a+2b+3c+4d=30 为例,使用遗传算法找到a b c d 值满足该等式。很显然可以使用这样一个函数衡量适应度
f (x) = |(a + 2b + 3c + 4d) - 30|
a b c d 初始化为0到30之间的一个自然数。
步骤一 初始化 (下面步骤不完全和算法步骤对应)
随机生成六个染色体Chromosome[1-6]。
Chromosome[1] = [a;b;c;d] = [12; 5; 23; 8]
Chromosome[2] = [a;b;c;d] = [ 2; 21; 18; 3]
Chromosome[3] = [a;b;c;d] = [10; 4; 13; 14]
Chromosome[4] = [a;b;c;d] = [20; 1; 10; 6]
Chromosome[5] = [a;b;c;d] = [ 1; 4; 13; 19]
Chromosome[6] = [a;b;c;d] = [20; 5; 17; 1]
步骤二 评估
计算每个染色体的适应度。
F_obj[1] = Abs(( 12 + 2*05 + 3*23 + 4*08 ) - 30) = 93
F_obj[2] = Abs((02 + 2*21 + 3*18 + 4*03) - 30) = 80
F_obj[3] = Abs((10 + 2*04 + 3*13 + 4*14) - 30) = 83
F_obj[4] = Abs((20 + 2*01 + 3*10 + 4*06) - 30) = 46
F_obj[5] = Abs((01 + 2*04 + 3*13 + 4*19) - 30) = 94
F_obj[6] = Abs((20 + 2*05 + 3*17 + 4*01) - 30) = 55
步骤三 选择
适应度是越小越好,我们将适应度取倒数(加1避免出现除以0的错误),并归一化得到一个概率P
Fitness[1] = 1 / (1+F_obj[1]) = 1 / 94 = 0.0106
Fitness[2] = 1 / (1+F_obj[2]) = 1 / 81 = 0.0123
Fitness[3] = 1 / (1+F_obj[3]) = 1 / 84 = 0.0119
Fitness[4] = 1 / (1+F_obj[4]) = 1 / 47 = 0.0213
Fitness[5] = 1 / (1+F_obj[5]) = 1 / 95 = 0.0105
Fitness[6] = 1 / (1+F_obj[6]) = 1 / 56 = 0.0179
总计 Total = 0.0106 + 0.0123 + 0.0119 + 0.0213 + 0.0105 + 0.0179 = 0.0845
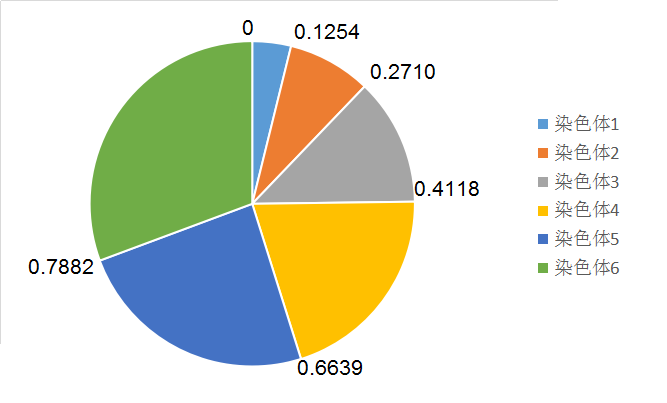
P[1] = 0.0106 / 0.0845 = 0.1254
P[2] = 0.0123 / 0.0845 = 0.1456
P[3] = 0.0119 / 0.0845 = 0.1408
P[4] = 0.0213 / 0.0845 = 0.2521
P[5] = 0.0105 / 0.0845 = 0.1243
P[6] = 0.0179 / 0.0845 = 0.2118
从结果可以看出基因4具有最高的适应度。接下来计算累计概率分布CPD:
C[1] = 0.1254
C[2] = 0.1254 + 0.1456 = 0.2710
C[3] = 0.1254 + 0.1456 + 0.1408 = 0.4118
C[4] = 0.1254 + 0.1456 + 0.1408 + 0.2521 = 0.6639
C[5] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243 = 0.7882
C[6] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243 + 0.2118 = 1.0
然后生成六个随机数R[i=1,2,3,4,5,6],通过这六个随机数在上图中的位置区间选择新的染色体,比如,当随机数在0.4118到0.6639之间则选择染色体4。不难看出,这种方法反应了适应度好的染色体具有更大概率被选择。
随机生成的六个随机数如果是:
R[1] = 0.201
R[2] = 0.284
R[3] = 0.099
R[4] = 0.822
R[5] = 0.398
R[6] = 0.501
那么相应的六个新的染色体是:
NewChromosome[1] = Chromosome[2] = [ 2; 21; 18; 3]
NewChromosome[2] = Chromosome[3] = [10; 4; 13; 14]
NewChromosome[3] = Chromosome[1] = [12; 5; 23; 8]
NewChromosome[4] = Chromosome[6] = [20; 5; 17; 1]
NewChromosome[5] = Chromosome[3] = [10; 4; 13; 14]
NewChromosome[6] = Chromosome[4] = [20; 1; 10; 6]
步骤四 交叉
假设交叉率为25%(0.25),那么生成6个随机数,如果随机数小于交叉数,则对应的染色体被选择用于交叉。比如随机数为:R[1] = 0.191, R[2] = 0.259, R[3] = 0.760, R[4] = 0.006, R[5] = 0.159,R[6] = 0.340。那么得到用于交叉的三对染色体是NewChromosome[1], NewChromosome[4] 和NewChromosome[5]。交叉方式为:
NewChromosome[1] >< NewChromosome[4]
NewChromosome[4] >< NewChromosome[5]
NewChromosome[5] >< NewChromosome[1]
下面决定从那个位置进行交叉。因为染色体长度为4,则随机生成1-(4-1) 大小的随机数,随机数用于表示基因从哪里开始交叉。
C[1] = 1 C[2] = 1 C[3] = 2
CrossChromosome[1] = [ 2; 21; 18; 3] >< [20; 5; 17; 1] = [ 2; 5; 17; 1] // C[1] = 1
CrossChromosome[2] = [20; 5; 17; 1] >< [10; 4; 13; 14] = [20; 4; 13; 14] // C[2] = 1
CrossChromosome[3] = [10; 4; 13; 14] >< [ 2; 21; 18; 3] = [10; 4; 18; 3] // C[3] = 2
那么剩余的种群中则有染色体:
NewChromosome[2] = [10; 4; 13; 14]
NewChromosome[3] = [12; 5; 23; 8]
NewChromosome[6] = [20; 1; 10; 6]
CrossChromosome[1] = [ 2; 5; 17; 1]
CrossChromosome[2] = [20; 4; 13; 14]
CrossChromosome[3] = [10; 4; 18; 3]
步骤五 突变
假设突变概率为10%(0.1)。考虑到6个染色体中每个有6个基因,那么将有4×6×0.1= 2.4 ≈ 2个基因发生突变,通过产生两个1-24范围的数值得到突变染色体位置(假设为12和18)。接着还产生两个1-30之间的随机数作为突变后的结果(假设为2 和 5)。那么得到新的种群如下(红色为突变基因):
Chromosome[1] = [10; 4; 13; 14]
Chromosome[2] = [12; 5; 23; 8]
Chromosome[3] = [20; 1; 10; 2]
Chromosome[4] = [ 2; 5; 17; 1]
Chromosome[5] = [20; 5; 13; 14]
Chromosome[6] = [10; 4; 18; 3]
步骤六 回到步骤二进行迭代
步骤七 至循环代数次结束
步骤六和步骤七类似,不再赘述。
整个过程如下图所示:
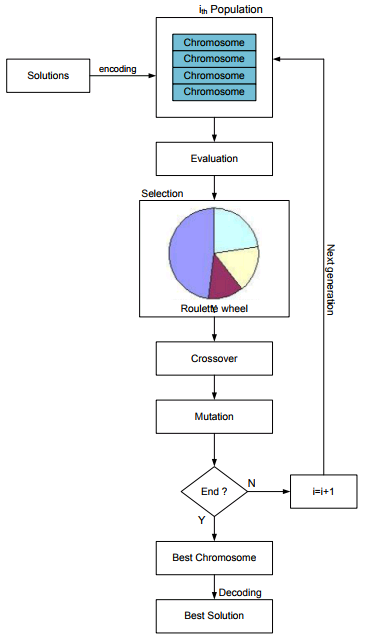
一个监督的赫布学习(Hebb Learning)的例子
赫布学习(Hebb Learning)基于赫布规则(Hebb Rule):
When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of cells firing B, is increase.
赫布规则大致说的是如果神经细胞刺激不断加强,两者联系加强。
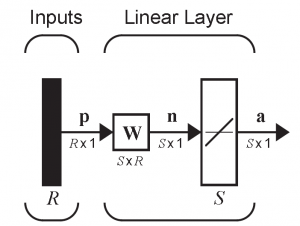
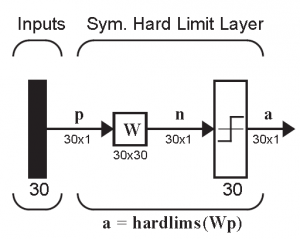
首先看看一个简单的神经网络的结构(以识别为例):
左边P(R×1的向量) 是输入,表示待识别物体的R 个特征。W是权重矩阵,通过计算特征和权重矩阵的乘法,用于形成S 个结果,S是判别函数。最终形成a (S×1向量)的结果。下面以位矩阵的数字识别为例:
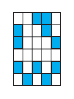
问题:有6×5大小的像素矩阵用于表示数字0,1,2,如下图所示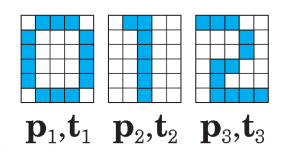
每个数字矩阵用一个一维的特征向量表示,比如0 对应的特征向量为p1:
p1 = [-1 1 1 1 -1 1,-1 -1 -1 1 1 -1 -1 -1 1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]^T
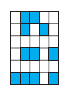
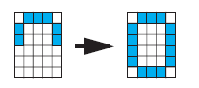
其中-1代表这个像素不上色,1反之,t1-t3分表代表结果是0,1,2。那我们的问题是如果识别带有误差,或者只有部分像素的例子。如下面图中应该识别为多少呢?
分析:使用如下的神经网络,
权重矩阵W通过下面等式计算:
W = p1·p1^T + p2·p2^T + p3·p3^T
在我们这个例子里,权重函数如下
S判别函数我们使用hardlims,当输入大于0则结果为1,当小于0 则结果为-1. 针对一个特定识别过程(如下图):
下面是实现这个过程的Python 代码,使用到numpy 库。
#_*_coding:utf-8_*_
import os
import sys
import numpy as np
mat0 = np.matrix([-1,1,1,1,-1,\
1,-1,-1,-1,1,\
1,-1,-1,-1,1,\
1,-1,-1,-1,1,\
1,-1,-1,-1,1,\
-1,1,1,1,-1])
mat1 = np.matrix([-1,1,1,-1,-1,\
-1,-1,1,-1,-1,\
-1,-1,1,-1,-1,\
-1,-1,1,-1,-1,\
-1,-1,1,-1,-1,\
-1,-1,1,-1,-1])
mat2 = np.matrix([1,1,1,-1,-1,\
-1,-1,-1,1,-1,\
-1,-1,-1,1,-1,\
-1,1,1,-1,-1,\
-1,1,-1,-1,-1,\
-1,1,1,1,1])
mat0t = mat0.getT()
mat0p = mat0t.dot(mat0)
mat1t = mat1.getT()
mat1p = mat1t.dot(mat1)
mat2t = mat2.getT()
mat2p = mat2t.dot(mat2)
print "===============matrix 0===================="
print(mat0p)
print "===============matrix 1===================="
print(mat1p)
print "===============matrix 2===================="
print(mat2p)
matw = mat0p+mat1p+mat2p
print "===============matrix sum===================="
print matw
testa0 = np.matrix([-1,1,1,1,-1,\
1,-1,-1,-1,1,\
1,-1,-1,-1,1,\
-1,-1,-1,-1,-1,\
-1,-1,-1,-1,-1,\
-1,-1,-1,-1,-1])
mata0 = matw.dot(testa0.getT())
print "=========== raw mata0 =============="
print mata0
for ii in xrange(mata0.size):
if mata0[ii] > 0:
mata0[ii] = 1
else:
mata0[ii] = -1
print "============= After testa0 ================="
print mata0
备注:这是Neural Network Design 的一个例子,作者用python 代码实现了下。