Clay Codes ( Clay Codes: Moulding MDS Codes to Yield an MSR Code ) 是FAST18 上提出的一种编码方法,文章地址,Clay 码能够将一般的MDS 码(最优容错)转化为具有最优修复的编码方法,具有以下性质:
- Minimum Storage (最小存储开销,同经典RS码和最小存储再生码,MSR)
- Maximum Failure Tolerance(最大容错,即 (n,k)-Clay 码可以容任意n-k 失效)
- Optimal Repair Bandwidth (最优修复开销,能够达到理论最优值)
- All-Node Optimal Repair (最小开销修复所有节点的数据,包括原始数据和校验数据)
- Disk Read Optimal (最优磁盘读)
- Low Sub-packetization (低分包数,即码字长度短)
首先介绍下Clay 码的设计思想,第二部分从生成矩阵的角度来看看Clay 码如何实现。
一 Clay 码的设计思想
1.1 术语
首先文章介绍了一些基础概念:
纠删码:纠删码将一段原始数据等分为k 份,进而编码为m 份,共计n=k+m 份,通过将这n 份数据分别存储在n 个不同的存储节点上,达到抵御数据丢失的风险。
标量码/向量码(Scalar code/Vector code):标量码每个码字在每个节点上包含一个字节,向量码在每个节点上包含若干个字节,共同组合为一个超字节(superbyte),不同节点上超字节共同组成一个码字。
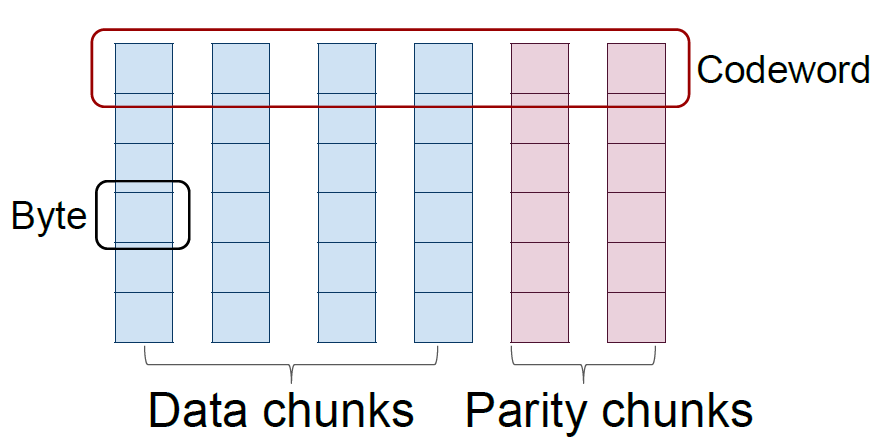
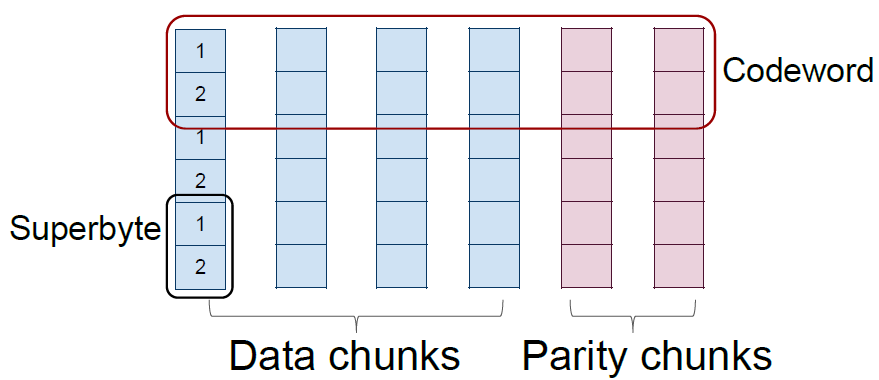 上图表示标量码,下图表示向量码。在磁盘阵列中,每个条带(stripe)也是横跨n 个节点,对应的一个码字,而码字中一个字节(标量码)或者超字节(向量码)则对应着条带中的一个数据块。一个(n,k) 标量码和向量码在生成矩阵中对应的是一个n×k 和nw×kw 矩阵,其中一个超字节包含w 个字节。
上图表示标量码,下图表示向量码。在磁盘阵列中,每个条带(stripe)也是横跨n 个节点,对应的一个码字,而码字中一个字节(标量码)或者超字节(向量码)则对应着条带中的一个数据块。一个(n,k) 标量码和向量码在生成矩阵中对应的是一个n×k 和nw×kw 矩阵,其中一个超字节包含w 个字节。
MDS 码:最大距离可分(Maximum Distance )码是一种最优容错编码方法,即编码后的n 份数据最大可容忍任意m 份数据失效,原始数据也不会丢失。常见的RS、CRS、Evenodd、RDP 码都是MDS 码。
修复开销:修复开销指的是重建一个节点数据或单个数据块所需要的数据量(从磁盘读取、从网络传输的数据量)。在存储系统中,单点失效是常态,因此研究更注意单点失效的修复开销。
MSR 码:最小存储再生码(Minimum Storage Regenerating codes,MSR 码)是一类具有最小存储开销下的再生码。再生码是一类能够减少修复开销的纠删码。
原始数据量为M,再生码在每个节点存储的数据量为α。如果每个节点存储量最小,即α=M/k,那么这个再生码是MSR 码,和其他经典(n,k)-MDS 码存储开销相同。当一个节点失效,需要从剩余d<(n-1) 个节点中每个取β<α 数据完成修复,修复开销为dβ。当n-1 时,修复开销最小,为(n-1)α/m。
磁盘开销:再生码是网络编码研究者提出的,在数据修复时在网络上传输的数据量能够达到理论最小,但需要在磁盘上读取大量数据,进而计算得到少量修复数据进行数据修复,因此需要额外的磁盘访问和计算。Clay 码能够减少磁盘开销,即在网络上传输的数据就是从磁盘哦读取的数据。
系统码:系统码编码后保留了原始数据,非系统码编码后只有校验数据。实际存储系统中常见的是系统码,这样数据读取不用解码。
1.2 编码方法
下面以(n=4,k=2) 来介绍Clay 码,一种将一般MDS 码转化为MSR 码的方法。
Clay 是Coupled Layer 的结合,包含了Clay 码的两个特点:1 将MDS 码分层处理;2 分层之间耦合数据。
一个(4,2)-MDS 码编码后的数据有4 份,可以摆放成一个正方形。
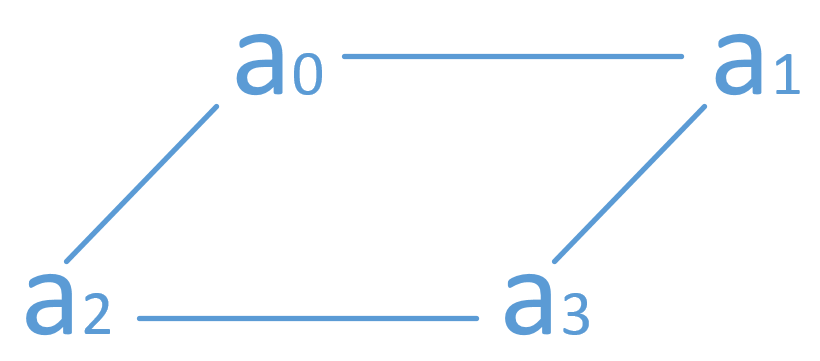
四个(4,2)-MDS 码编码后的数据可以形成一个四层的棱柱,四棱柱的四个边对应着四个存储节点,边上的四个点所代表的数据存储于同一个节点。(下图a_0/b_0/c_o/d_0 都存在同一个节点)
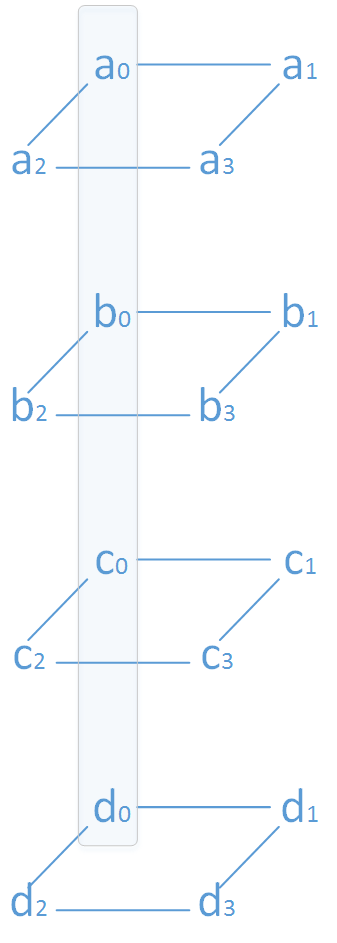
耦合是将分层中不同数据进行线性组合,以实现最小修复开销。
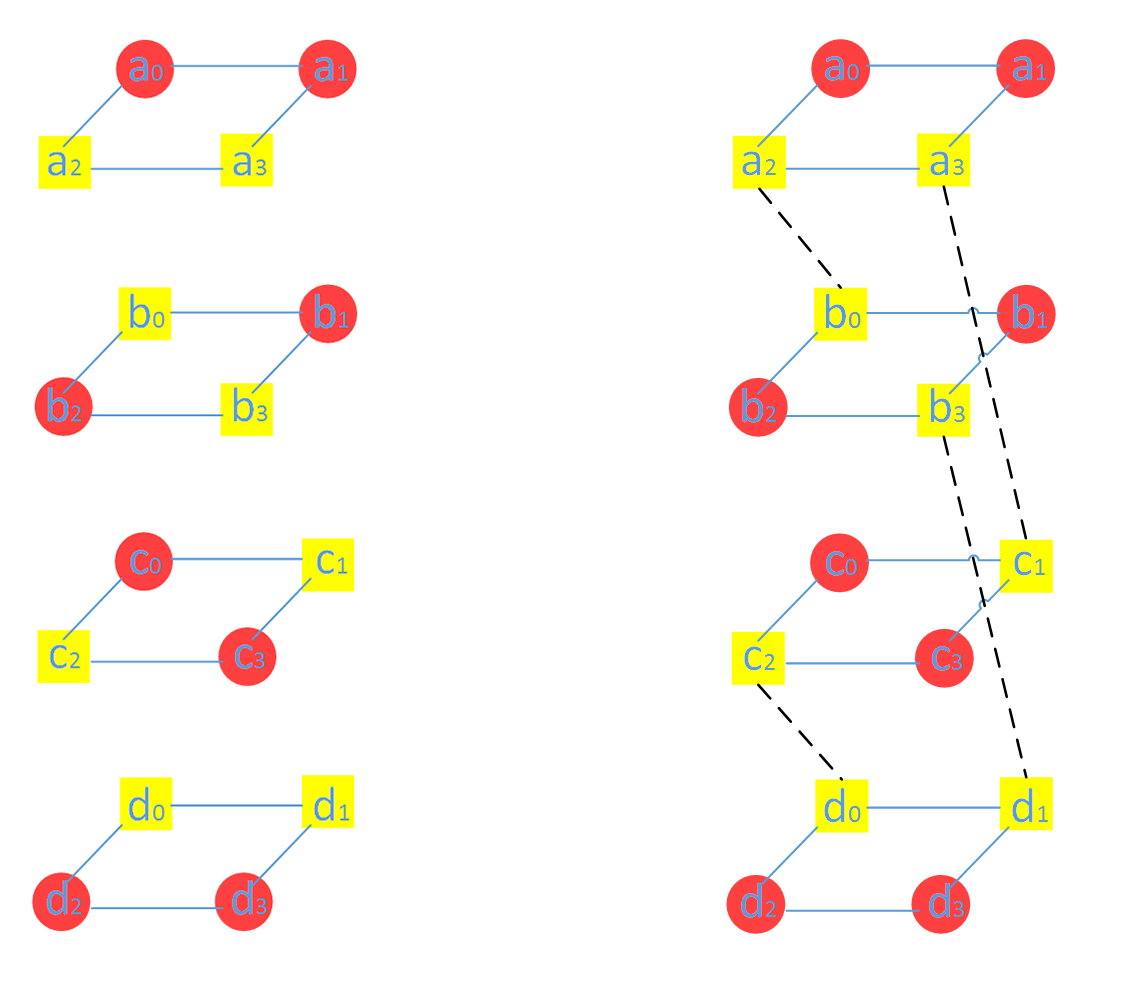
图中被耦合的数据块用黄色表示,没有参与耦合的数据块用红色表示,两两耦合对应的数据块如上右图所示。如何选择耦合的数据块对文章中有也介绍,但为什么这样选择文章未提及。
下面谈谈什么是耦合,耦合即通过线性组合两个数据块,不管这两个数据块是原始数据块还是校验数据块。然后再将两个线性组合后的数据块(Coupled)取代两个原来未耦合的数据块(Uncoupled)。下图中(a_0, b_0),[a_0,b_0] 表示的就是数据块a_0 和b_0 的线性组合。注意:实际中Clay 码在节点上存储的是耦合后的数据,这样才能保证Clay 码的最优修复。
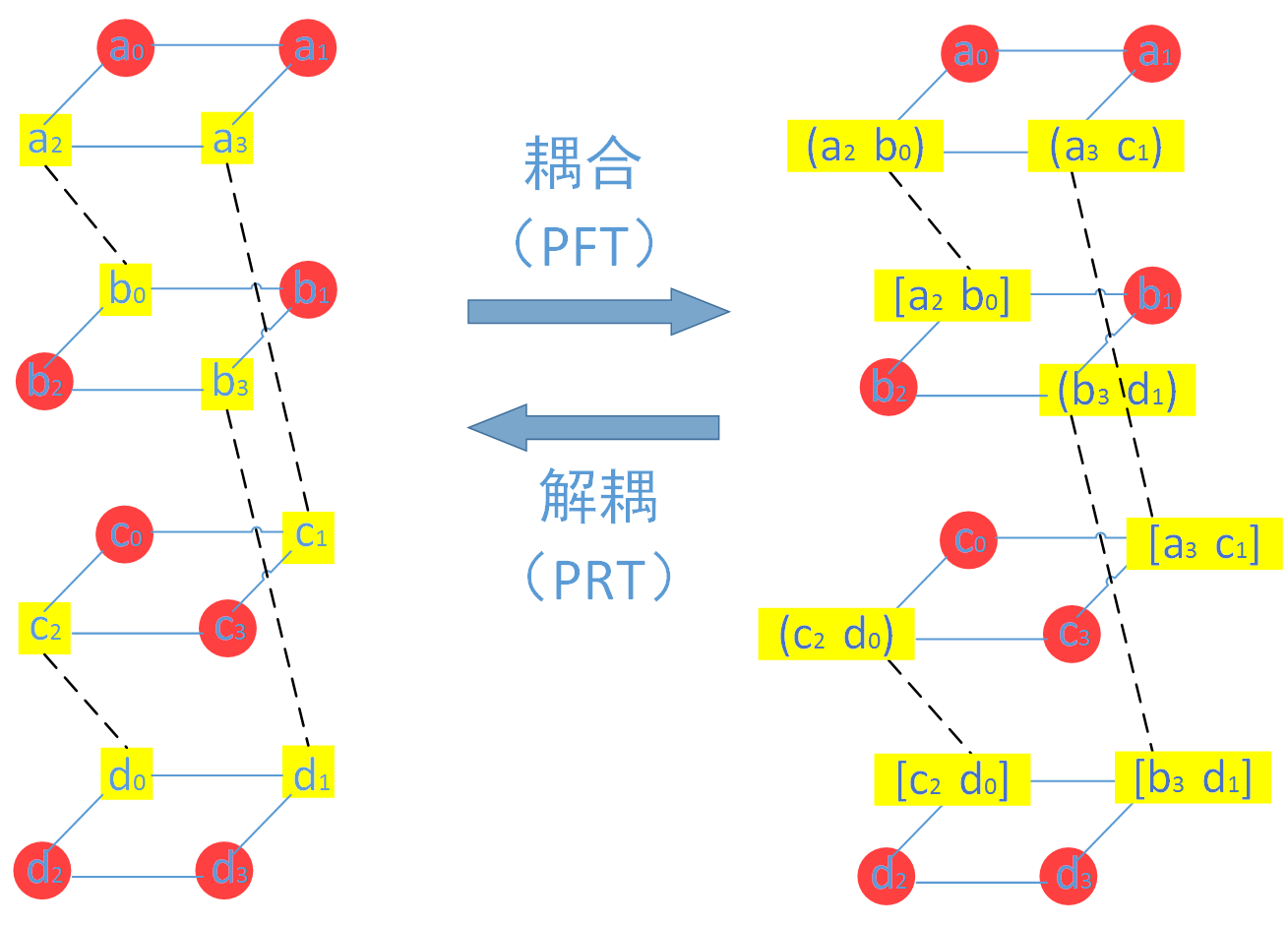
两个数据块的线性组合可以表示为数据块的乘法,解耦同理,如果用C(p) C*(p)表示两个耦合的数据块,解耦即乘以解耦矩阵,
![]()
γ 为不等于0的值,使得矩阵(在对应的有限域)满秩即可,比如2。
1.3 最优修复单点失效
下面以一个节点的修复来展示Clay 的最小修复开销,(4,2) 编码最小修复开销为(n-1)α/m = 3α/2 = 6,这也是其他MSR 的最小理论修复开销。下图给出了原a_2 数据块所在节点的修复过程。
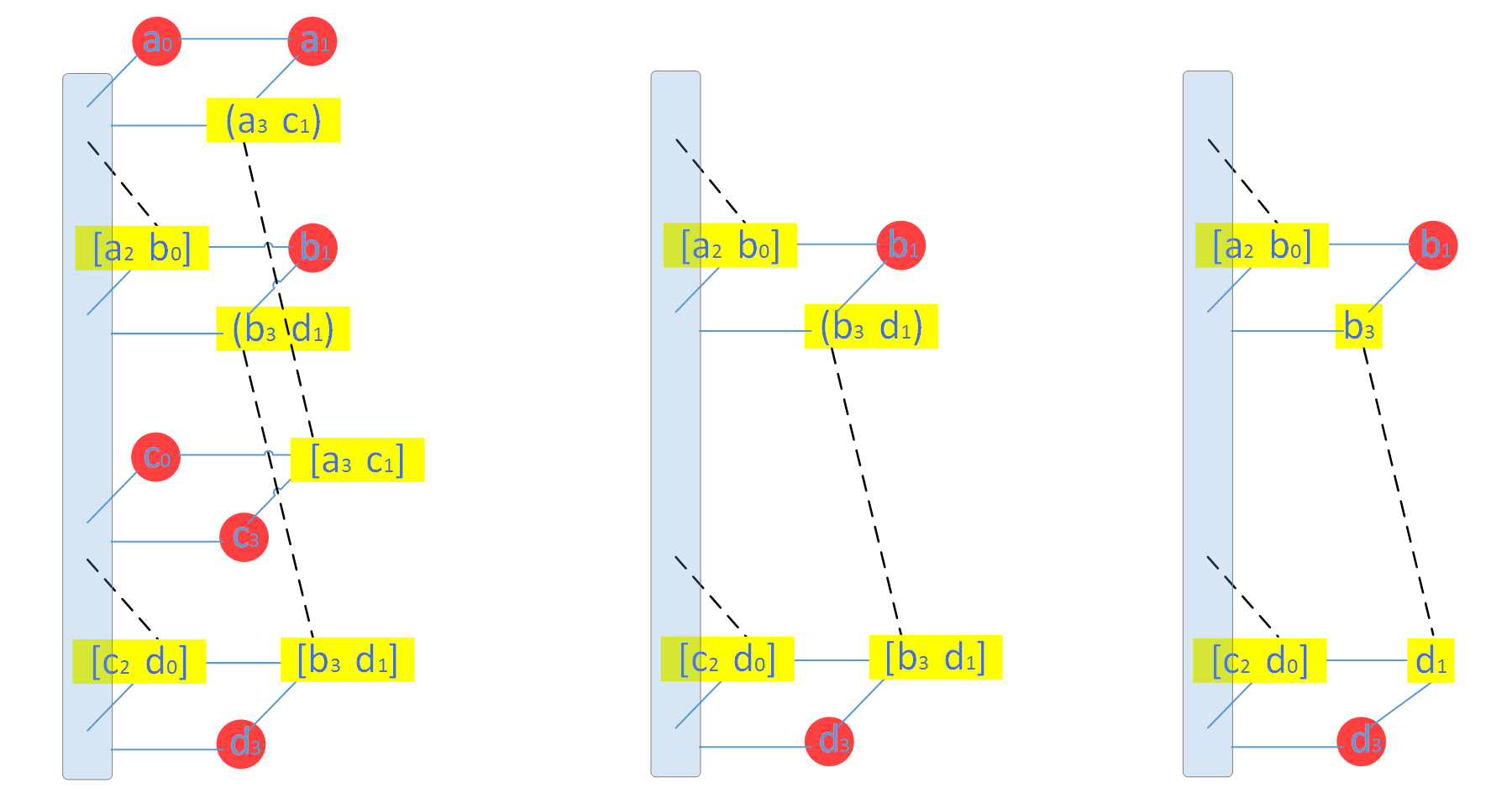
Clay 修复该节点失效只需要第二层和第三层的剩余数据块(如上图(中)所示),修复步骤如下:
- 两个耦合的数据块(b_3,d_1) 和[b_3, d_1] 解耦得到b3 和d1,如上图(右)
- 第二层通过b1,b3 的MDS 解码得到b_0, b_2,第四层MDS 解码得到d_0,d_2
- 利用第二层中[a_2, b_0] 和步骤2 得到的b_0 得到a_2,同理得到c_2;
简单推导可以发现其他三个节点也可以以最小开销完成数据修复。
1.4 系统码
需要注意的是Clay 码这时虽然满足了所有节点的最优修复,但耦合的过程中某些数据已经不再是系统码,因为某些原始数据已经线性组合为校验数据。作者因此提出了一种“耦合-编码-再解耦”的方式来保证Clay 码的系统性(systematic),如下图所示。
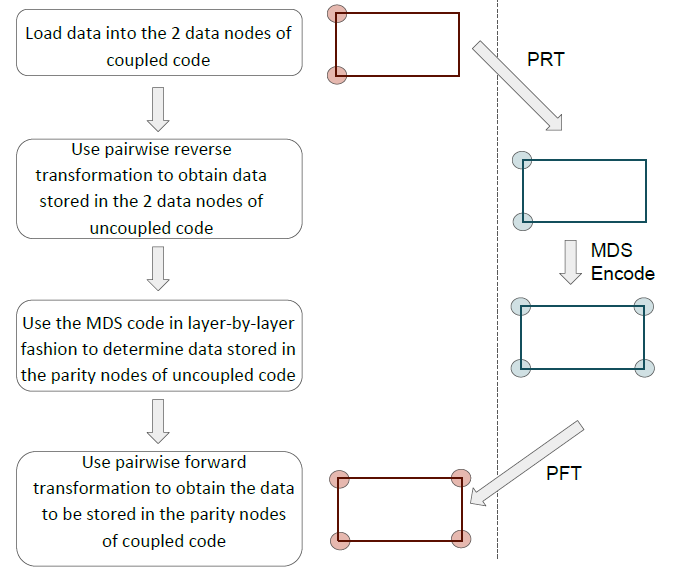 首先对原始数据进行耦合,经过MDS 编码后再解耦,这样原始数据还是原始数据,但校验数据不再是MDS 编码后的校验数据了。
首先对原始数据进行耦合,经过MDS 编码后再解耦,这样原始数据还是原始数据,但校验数据不再是MDS 编码后的校验数据了。
但如果是这样理解的话,会存在一个问题:MDS 编码前,耦合的校验数据为空,导致一个原始数据和空数据耦合,那么解耦后的数据能延续刚才的最优修复么?
换个角度,如果耦合的两个数据块中有一个是原始数据,是不是可以选课合适的耦合方程来保证原始数据不发生变化,即数据块a,b 耦合后可以是a,xa+yb(a 是原始数据)或xa+yb,b(b是原始数据)的形式么?但如果需耦合数据都是校验数据块呢?
这几个问题可以通过生成矩阵的方法来解释。
二 Clay 码的生成矩阵
本节用生成矩阵这个工具来展示如何实现Clay 码,即生成(4,2)-Clay 码的生成矩阵并验证其最优修复性质。
首先利用Clay 码“耦合 – MDS编码 – 解耦” 的变换过程构建其生成矩阵。因为三个变换都是线性变换,所以可以用三个矩阵来代替。
注意:前面我们提到解耦矩阵和耦合矩阵是互逆的,这是针对两个需要耦合/解耦数据块而言的,本节所讲的耦合、解耦矩阵是针对所有数据块,且需要在中建添加MDS 编码过程,所以本节耦合、结构矩阵大小不同,更不互逆。
|G| 是Clay 码的生成矩阵,那么
|G| = |U|×|GM|×|C|
|U|是解耦矩阵,|GM| 是MDS编码的生成矩阵,|C| 是耦合矩阵。
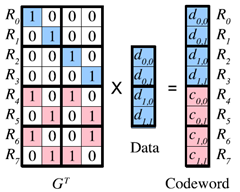
首先从最简单的MDS 编码矩阵 |GM| 开始,一层MDS 编码生成矩阵是一个2×2 单位矩阵和2×2 校验矩阵组合得到的4×2 的生成矩阵(如下左图所示)。四层的MDS 编码矩阵如下右图(在生成矩阵右边标出了该行向量对应的数据块)。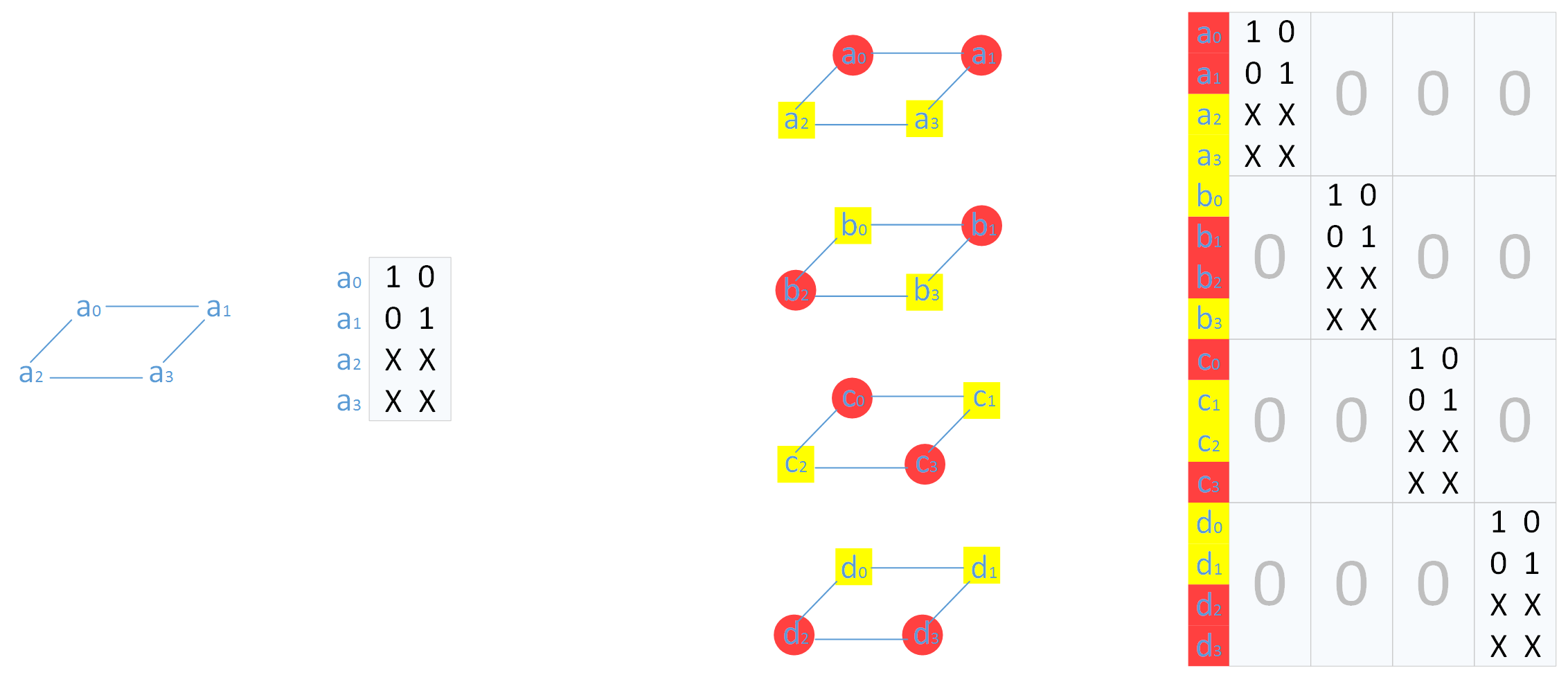
为了使得一个码字中原始数据部分放在一起,可以进行一个对齐操作,即将单位矩阵放在上面,新的生成矩阵为|GM|。
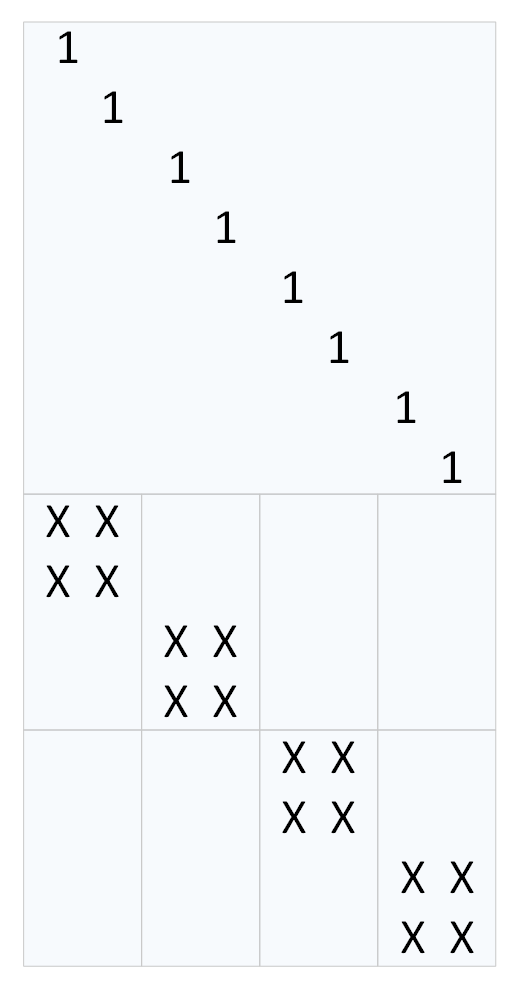
根据所对应数据块位置和耦合规则,可以得到解耦矩阵 |U|,如下图所示。

因为MDS 编码后,有16个数据块,所以解耦矩阵|U| 大小为16×16。
耦合矩阵是一个8×8 大小的矩阵(因为四层MDS码有8 个原始数据块,|GM| 大小是16×8)。那么利用|G| 矩阵上半部分是单位矩阵可解出耦合矩阵|C|
|G| = [I P] = |U|×|GM|×|C| → |C| = |I+L×GP|^{-1}
耦合矩阵|C| 是 |I+L×GP| 的逆矩阵,L 是解耦矩阵|U| 右上分块矩阵,GP是MDS 编码生成矩阵|GM| 下半部分的校验部分。
下面介绍程序验证过程。首先是测试当λ=2 时,两个数据块的耦合和解耦矩阵。
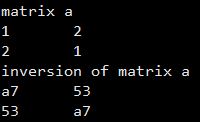
当λ=2 时,计算得到的耦合矩阵|C| = |I+L×GP|^{-1} 为

MDS 码采用RS码,|GM| 为
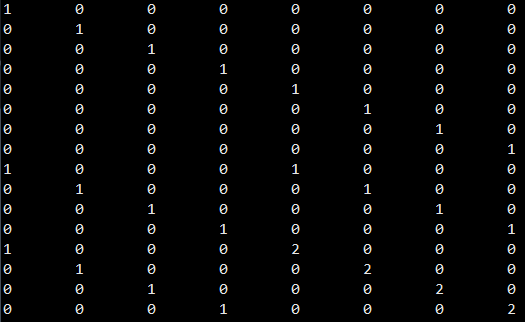
耦合矩阵乘积为 |GM|×|C| 为
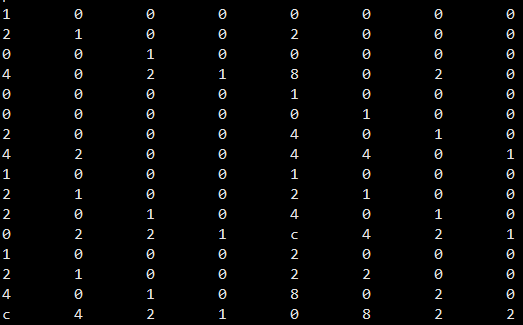
最终(4,2)-Clay 码生成矩阵|G|为
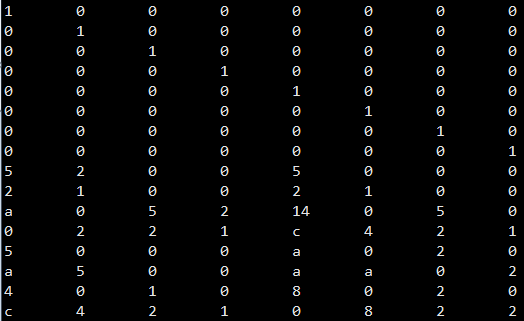
最后,用程序验证了这个矩阵的最优修复性质,具体而言,首先将该矩阵等分为4×8 的4个子矩阵,依次失效每个子矩阵,从失效子矩阵以外的矩阵中选取行向量重建该失效子矩阵,所需要选取的子矩阵的行向量个数即需要重建数据块的数量,验证发现所有子矩阵修复都只需要6 个行向量,达到了最小修复开销。