原文

本文作者是NCCloud 作者在INFOCOMM13 上发表的短文。作为NCCloud 的理论基础，证明了n = k+2 = d+1 情况下，FMSR 的存在性，并给出了这类编码的一个确定的编码方式。NCCloud 和本文提到的FMSR 具有三点重要性质：

1. FMSR 码存储效率和容错效率与MDS 相同
2. FMSR 达到最小修复带宽
3. FMSR 使用非编码修复（uncoded repair/repair-by-transfer）

下面对FMSR（n = k+2 = d+1）的存在性进行证明：

定义

---

MDS 性质：n 个节点中任意k 个节点，其中k(n-k) 个编码块可以解码为k(n-k) 个原始数据块。

 

可解码性（Decodability）：n 个节点中存在解码出k(n-k) 个原始数据块的k(n-k) 个编码块。

 

RBC(Repair Based Collection) ：一个RBC 是按照下面三个步骤选取的k(n-k) 个编码块的集合：

1. 从n 个节点中选择n-1 个节点
2. 从n-1 个节点中选择k-1 个节点，并从其中每个节点中选择全部n-k 个编码块
3. 从剩余n-k 个节点中每个节点选择一个编码块

不难计算出总计有 个不同的RBCs

 

LDC（Linear Dependent Collection）：假设一个RBC 在第2 步选择的k-1 个节点中包含了最新被修复的那个节点，那么当且仅当这个RBC 可以少于k(n-k) 个编码块的线性组合时，我们称其为LDC。

 

rMDS 性质（repair MDS）：排除所有LDCs，全部RBCs 都可解码，则rMDS 性质满足

 

引理

---

引理一：修复过程中，F 代表生成n-k 个新的编码块，而从n-1 个节点中选取的n-1 个的编码块，如果一个包含了新修复节点的RBC （用R 表示）是LDC，用Q 代表其第3 步选取的n-k 个节点，那么F 和Q 包含两个或者两个以上的共同编码块。

证明：不失一般性，假设节点1 失效，令P 为RBC 第2 步对应的k-2 个节点（排除新修复节点1 和其n-k 块编码块）。那么R = {P’_1,1,…, P’_1,n-k } U P U Q ，因为P’_1,1,…, P’_1,n-k 可以写成F 的线性组合，也就是R 包含了F U P U Q 线性组合的块。

F 包含了n-1 个节点中的各一个编码块，所以|F| = n-1；P 包含了RBC 中除去节点1 的其余k-2 个节点，所以|P| = k-2；|Q| = n-k。因为P 和Q 分别是RBC 第2 步和第3 步选择出来的，所以|P ∩ Q| = |F ∩ P ∩ Q| = 0。于是我们有|F U P U Q| = |F| + |P| + |Q| – |F ∩ P| – |F ∩ Q| – |P ∩ Q| + |F ∩ P ∩ Q| = n-1 + (k-2)(n-k) + n-k – (k-2) – |F ∩ Q| – 0 + 0 。 因为是LDC，所以|F U P U Q| < k(n-k) ，因此|F ∩ Q| ≥ 2。得证                                  ■

引理一给出了LDC 的另一个性质（或者说是定义LDC 的条件）。LDC包含新修复节点作为RBC 选择k-1 个节点之一，并且包含2 个或2 个以上用于修复新节点的编码块。

引理二：假设第r 轮修复后，rMDS 性质满足。那么对于n 个节点中的n-1 个节点，我们总能从这n-1 个节点中每个选择出一个编码块，使得任意一个RBC 包含n-1 个编码块总是可解码的。

证明：不失一般性，假设从节点2,…,n 个节点中各选一个编码块的集合为G，该引理的证明即是证明G 的存在性，如果RBC R 包含G，则R 是可解码的。

如果节点1 是第r 轮新修复的节点，那么R 根据LDC 的定义一定不是LDC，因为rMDS 性质，R 是可解码的。

如果节点1 不是第r 轮新修复的节点，不失一般性，假设节点2 是第r 轮修复的节点。假设修复节点2 的F = {P_1,f(1), P_3,f(3), …, P_n,f(n)} ，因为每个节点有n-k≥2 个编码块，可以构建G = {P_1,g(1), P_3,g(3), …, P_n,g(n)} 满足g(i) ≠ f(i) 其中i = 3,…n（g(2) 可以随机选取），如果R 包含G，那么在R 构建的第3 步，所有n-k 个块将从G 中选取，从而和F 没有交集，根据引理一，R 不是LDC。因此rMDS 满足，R 是可解码的。                                                ■

引理三证明中给定了一种选取用于修复r+1 轮失效节点的候选编码块的方法。

引理三：（Schwartz-Zippel 定理）参考这里 ，不再单独说明。

证明略。

定理一：假设一个文件使用k=n-2 的FMSR 进行编码。在第r 轮修复节点j 中，使用剩余节点中每个节点中的一个编码块，共计n-1 块编码块进行线性组合，那么通过增大域的大小F_q修复后的文件仍然满足MDS 和rMDS 性质的概率可以无限接近于1。

证明：使用归纳法证明。初始我们使用Reed-Solomon 码将文件编码为n(n-k) = 2n 块编码块，并且满足MDS 和rMDS 性质。假设在第r 轮修复后，MDS 和rMDS 性质都满足（这是我们的归纳假设）。

假设U_r = {P_1,1 , P_1,2 ; . . . ;P_k+2,1, P_k+2,2} 是第r 轮修复后的2n 个编码块。在第r+1 轮修复中，不失一般性，假设节点1 是失效节点。因为U_r 满足rMDS 性质，那么我们从引理二可以有以下推论。

推论 存在从节点2, …,n中选择的n-1 个编码块，表示为F = {P_2,f(2), . . . ,P_k+2,f(k+2)}，任何包含F 的RBC 是可解码的。

我们使用F 取修复节点1，假设修复节点1 生成新的编码块为{P’_1,1, P’_1,2}，那么：

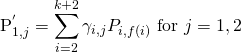
下面我们将证明总能够调整域F_q 中γ_i,j 使得在r+1 轮中修复后的编码块U_r+1 = {P’_1,1 , P’_1,2 ; . . . ;P_k+2,1, P_k+2,2} 仍旧满足MDS 和rMDS 性质，证明包含两部分：

部分一：U_r+1 满足MDS 性质。 因为U_r 满足MDS 性质，所以我们只需要保证剩下n-1 个节点{2,…,n} 中任意k-1 个节点子集合{s₁,…,s_k-1} 和修复的节点1 都是可解码的。不失一般性，我们假设{s₁,…,s_k-1} = {2,…,k}，其他情况都是对称的。

令V = {P_2,1, P_2,2 ; . . . ;P_k,1, P_k,2; P’_1,1 , P’_1,2 } 是节点1 到k 上的编码块，根据下面等式

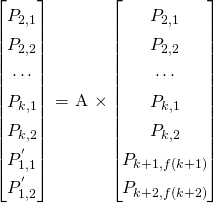
可以知道，V 中每个块都是一个RBC R 的线性组合，R={P_2,1, P_2,2 ; . . . ;P_k,1, P_k,2; P_k+1,f(k+1), P_k+2,f(k+2)}，其中A 是一个k(n-k)×k(n-k) 的编码矩阵：

因为R 是一个包含了F 的RBC，根据引理二它是可解码的。A 的行列式det(A) 根据引理三是可以任意概率不为0。因为R 可解码和A 是满秩的，那么V 可解码，也就是说U_r+1 满足MDS 性质。

部分二：U_r+1 满足rMDS 性质。由rMDS 的定义，我们需要证明第r+1 轮所有除了LDCs 以外的RBCs 都是可解码的。根据RBC 的定义，我们考虑两种RBCs，我们假设节点1 是修复的节点。

情况一：假设节点1 在RBC 选择第2 步作为k-1 个全选节点之一。假设在第1步，一个RBC 选择了n-2=k 个存活的节点，表示为{s₁,…,s_k} 属于{2,…,n}。那么在第2 步，RBC 继续选择k-2 个节点，表示为s₁,…,s_k-2 ，RBC 包含了这k-2 个节点和新修复节点1的所有编码块。最终在第3 步，RBC 从剩余的节点s_k 和s_k-1 中各选一块，表示为和。不失一般性，表示为{s₁,…,s_k} = {2,…, k-1} 并且(s_k , s_k-1) = (k, k+1)。

RBC 可以表示为R₁ = {P_2,1, P_2,2; . . . ; P_k-1,1, P_k-1,2; P’_1,1,P’_1,2; P_k,g(k),P_k+1,g(k+1)}，根据节点1 的修复过程，R₁ 可以写成X 的线性组合，X = {P_2,1, P_2,2 ; . . . ; P_k-1,1, P_k-1,2; P_k,g(k),P_k,f(k) ; P_k+1,g(k+1) ,P_k+1,f(k+1) ; P_k+2,f(k+2)}。

我们的目标是如果R₁ 不是一个LDC，那么它是可解码的。从引理一我们知道如果R₁ 是一个LDC，那么R₁ 第三步选择的块至少有两个编码块属于F = {P_2,f(2), . . . ,P_n,f(n)}（这些是用来第r+1 轮修复节点1 的数据块），也就是说P_k,g(k) =P_k,f(k) 和 P_k+1,g(k+1) = P_k+1,f(k+1) 。为了证明R₁ 不是LDC 的话则可解码将讨论(a) g(k) ≠ f(k) 和g(k+1) = f(k+1)，(b)  g(k) = f(k) 和g(k+1) ≠ f(k+1)，(c) g(k) ≠ f(k) 和g(k+1) ≠ f(k+1)。

考虑(a) ，我们将X 归约到{P_2,1, P_2,2 ; . . . ; P_k-1,1, P_k-1,2; P_k,1,P_k,2 ; P_k+1,f(k+1) ; P_k+2,f(k+2)}。那么X 是一个包含了F 的RBC。根据推论X 是可解码的，因此，R₁ 是一个可解码编码块集合的线性组合。同样地我们可以通过部分一的方法找到对应的系数γ_i,j 保证R₁ 是可解码的。证明(b) 和证明(a) 类似。

下面考虑(c)，X 归约为{P_2,1, P_2,2 ; . . . ; P_k-1,1, P_k-1,2; P_k,1,P_k,2 ; P_k+1,1 ,P_k+1,2 ; P_k+2,f(k+2)}。定义X = X – {P_k+2,f(k+2)}。注意到X 根据递归假设是满足MDS 性质的，因此X 是可解码的，意味着P_k+2,f(k+2) 可以看成X 的线性组合。显然地，我们也能说X 是X 的线性组合。因此R₁ 也是可解码的组合X 的线性组合，基于以上讨论R₁ 是可解码的。

情况二：新修复节点1 是在RBC 选择第3 步作为n-k 个选择一个编码块的节点之一。假设RBC 选取的第一步，选择了任意n-2=k 个存货的节点，表示为{s₁, …,s_k} = {2, …,n}。在第2 步，RBC 继续选择了其中k-1 个节点的子集，记做{s₁, …,s_k-1} ，并选择该k-1 个节点所有的编码块。最后在第3 步RBC 分别从修复节点1 和另一个节点s_k 选择另外两个编码块 和。不失一般性，记{s₁, …,s_k-1} = {2, …,k} 和 s_k = k+1。

假设这个RBC 用R₂ = {P_2,1, P_2,2 ; … ; P_k,1, P_k,2 ; P’_1,g(1), P_k+1,g(k+1)} 表示，我们要证明的是，如果R₂ 不是LDC，那么R₂ 是可解码的。根据引理一，F 中编码块和RBC 在第三步所取的编码块之间没有超过一个相同的编码块。所以R₂ 一定不是一个LDC。我们只需要证明R₂ 是可解码的。

根据之前矩阵乘法的等式，R₂ 可以写成一些编码块集合的线性组合Y = {P_2,1, P_2,2 ; … ; P_k,1, P_k,2 ; P_k+1,f(k+1), P_k+1,g(k+1) ; P_k+2,f(k+2) }。假设g(k+1) ≠ f(k+1) 。定义Y = Y – {P_k+1,g(k+1)}， 因为Y 是包含F 的一个RBC，所以Y 是可解码的。因此P_k+1,g(k+1) 可以看做是Y 的线性组合，同理显然Y 也是Y 的线性组合。因此R₂ 也是可解码组合Y 的线性组合。基于以上讨论R₂ 也是可解码的。

综合情况一和情况二，我们推导出所有不包含LDCs 的RBCs 都是可解码的。所以U_r+1 满足rMDS 性质。定理一成立。                                                                                                    ■