Android 开发笔记（SDK）

Posted on by
回复

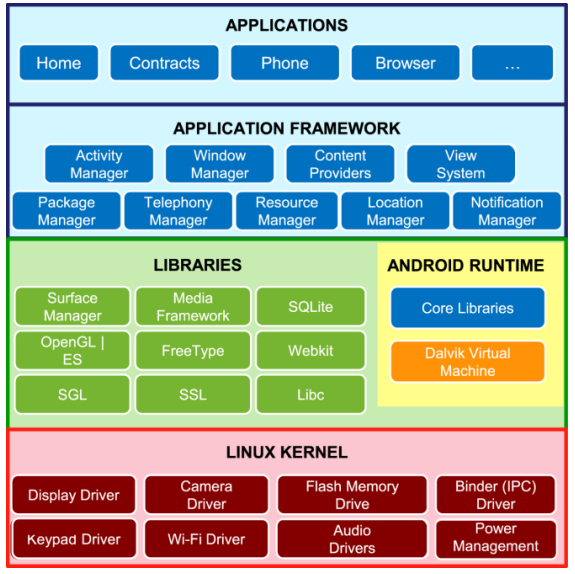
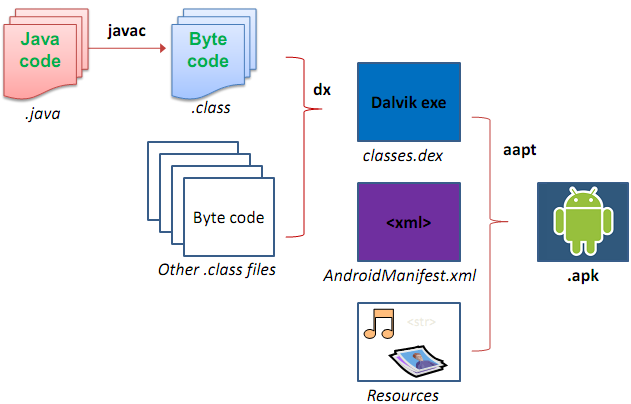
Android 为开发者提供的SDK（Software Development Kit，软件开发包）提供了一系列API，通过调用这些API 即可写出各具形态的app 了，所以我们应该对SDK 有一定的了解。

SDK 中Java 类以树层次结构打包，最上层的是android package，它主要包含了app 的资源类和对安卓系统的权限。如：Manifest  |  Manifest.permission  |  R  |  R.anim  |  R.array  |  R.attr  |  R.color  |  R.dimen  |  R.drawable  |  R.id  |  R.layout  |  R.string  |  R.style  |  R.xml 等。

android.app 中包含了android已封装好的一些高级类，如： Activity  |  Service  |  Fragment 。

Activity 类表示人机交互的一个界面。

Service 类表示一个后台长时间运行的组件，无UI，比如处理网络通信，音乐播放，或者是与一个content provider 交互。

Fragment 类在平板等大屏显示时表示activity 行为的一部分，并且关联相应的UI（可以看做是一部分UI，类似于activity）。

adroid.app 中还包含了其他类和接口：Dialog  |  ActionBar  |  Notification 等。

 

提供基础的操作系统级别的服务：services， message passing，IPC(Inter-Process Communication)。

BatteryManager 电池状态信息。

Bundle  一个从字符值到各种可打包类型的映射。

 

包含了可以访问android 提供content providers 的类。

 

包含app 外观设计的一些资源类：  R  |  R.anim  |  R.attr  |  R.bool  |  R.color  |  R.dimen  |  R.drawable  |  R.id  |  R.integer  |  R.layout  |  R.string  |  R.style  |  R.styleable 等。

 

提供了app 布局的一些小部件，如Bar 等。  AppBarLayout  |  NavigationView  等。

 

关于文字的类。有关接口和类： Editable  |  GetChars  |  Annotation  |  AutoText  |  Html  |  Layout

 

人如其名，包含一些小工具类，如时间、base64编码、字符串和数字处理方法等。

 

安卓app 上常用的一些UI 组件类。接口：Menu  |  ContextMenu  |  MenuItem  类：Display  |  Gravity  |  LayoutInflater (在对应的View 对象中实例化某个XML布局) |  MenuInflater  |  View(UI最基本的组件)

 

包含屏幕上使用的UI 组件，你也可以自己设计一些组件（实现View 的子类）。类：  Button  |  CheckBox  |  CheckedTextView  |  EditText  |  GridView  |  ImageButton  |  ImageView  |  LinearLayout  |  ListView  |  MediaController  |  ProgressBar  |  RadioButton  |  RadioGroup  |  RelativeLayout  |  Scroller  |  TableLayout  |  Toast  等。

 

包含了在设备上访问和写入数据的类，主要包括：1.内容分享 (android.content  中的 ContentProvider 、 ContentResolver 、Intent 和 IntentFilter)；2. 包管理（访问一个安卓包.apk的信息） 3. 资源管理（获取应用app 相关的资源数据，如strings，drawables，media等）。

 

包含用于处理从content provider 返回来的数据。如果需要管理一个私有的数据库，请使用 android.database.sqlite 类。

 

管理Sqlite 的类。接口和类：SQLiteCursorDriver  |  SQLiteClosable  |   SQLiteCursor  |  SQLiteDatabase  |  SQLiteQuery  |  SQLiteStatement  等。

 

提供可以在屏幕上直接画图的低级工具，如画布、滤镜、点和矩形。

 

提供管理可视化元素（图、灰度等）的类，这些类经常被widgets 作为背景图片或者指示器。

 

管理音频和视频的类。AsyncPlayer  |  AudioManager  |  MediaPlayer  |  Ringtone

 

java.net.* 之上的网络访问类。

 

使用OpenGL 画图。

 

 

 

 

Ubuntu14.04 上安装pygame

Posted on by
回复

因为在一台ubuntu 服务器上跑个pygame 的程序，在ubuntu14.04 上安装pygame 了一天，之前在windows 上安装很顺利，换做ubuntu 上就有点傻傻的。总结来说尽量不要手动下源包，通过configure 和 make install 来安装，因为存在很多依赖（32-bit，64-bit 等）的问题。应该采用正确的安装姿势：

sudo apt-get install python-game

我的过程如下：

在pygame 官网下载了最新（2009年的(⊙﹏⊙)b，因为基于的SDL 从1.2换做2.0版本了，无法做兼容了）的pygame 源码，解压， python setup.py install  安装。

安装后的结果是可以在程序中 import pygame 并使用基本的函数（如pygame.draw.line 等），但如果要使用相关其他模块时，如 import pygame.font 则会出现 font module not found的问题. 我尝试采用 http://stackoverflow.com/a/15368766/1424948 中的方法安装相关的模块：

$ sudo apt-get install python-dev libsdl-image1.2-dev libsdl-mixer1.2-dev  
libsdl-ttf2.0-dev   libsdl1.2-dev libsmpeg-dev python-numpy subversion 
libportmidi-dev ffmpeg libswscale-dev libavformat-dev libavcodec-dev

但是还是会存在  font module not found 的问题，我也尝试使用自动安装pygame的方法来解决：

$ sudo apt-get install python-pygame

但这个问题应该是之前的手动安装已经无法覆盖，而手动的安装依赖问题无法解决。最终我的解决方法是：

  1. sudo python setup.py clean
  2. 删除 python/site-packages 下的pygame 包
  3. sudo apt-get install python-pygame

完成这三步后，一切OK。

 

 

Android 开发笔记（准备工作）

Posted on by
回复

一、开发工具

  • Java 

Android 开发基于Java 语言，所以Java 语言环境必须安装。

  • Android SDK

Android SDK (Software Development Kit) 是开发Android 软件开发包，为开发者提供调用Android API调用，并负责将编译源码。功能类似于传统C++/MFC中开发的库文件加编译器。

从理论上讲，有Java 和Android SDK 就可以开发出结果为apk 的安卓应用了，但在目录、文件管理上比较困难，和其他工具（如模拟器）的扩展也需要手动操作，因此一般开发人员还需要一个开发平台。

  • Android Studio 或者Eclipse 开发平台

开发平台主要功能有三点：1.组织文件和目录；2.自动生成代码；3.扩展其他工具、插件。类似于Visual Studio平台中的管理功能，平台根据类型和作用分目录存放不同文件，比如res 存放静态文件。类似于使用MFC 新建项目时，VS 会自动生成一些通用代码。平台的另外一个好处就是很方便的能够扩展一些工具，比如模拟器，或者是在编译较老的SDK 时，需要从网上下载，平台都能够自动处理。总之，平台好处就是自动化处理一些原本需要人工操作的过程。

  • gradle

linux/C 项目开发中，如果你有了C语言环境（compiler，linker），有了项目所需要的库文件，你还需要通过一定的方法、规则将源文件生成安装程序，这些方法和规则一般写在Makefile 中，不同硬件设备有所区别，所以在安装源码时常通过configure 等脚本生成makefile，最后才make生成最终程序。Android 开发同理，一个Android 项目也需要通过SDK 的一些命令、工具生成中间文件，最后才生成安装程序，而管理这个过程最流行的工具就是gradle。当然不用gradle 也是可以的，只是需要手工敲得命令有些复杂和单调而已。

  • 模拟器（Emulator）

如果你没有真实的设备运行你的Android 程序，模拟器是不错的选择， 但平台中自带的模拟器效率较低，可以考虑其他模拟器，如Genymotion等。

二、安装过程

  1. 安装JDK（Java Development Kit）
  2. 安装Android SDK
  3. 安装Android Studio （下面全部以AS为例，需要VPN支持，或者使用SS并在AS 配置代理）
  4. 安装Android Emulator

三、Android体系结构

Android 基于Linux 操作系统的一个重要原因就是Linux 内核具有良好的硬件设备的支持，比如用于存储的磁盘，用于无线网连接的wifi。通过公共库（Libraries）对底层硬件的封装，为应用框架（Application Framework）和Android Runtime 提供了更具有特色的功能，比如SQLite 提供结构化数据库存储，OpenGL 提供高性能画图等。Android Runtime 基于优化的Java 虚拟机，称作Dalvik Virtuak Machine，任何Android 应用都是运行在这个虚拟机之上，虚拟机可以为应用分配内存和处理进程和进程间通信。应用框架（Application Framework）为程序提供更高层次的工功能服务，比如资源的访问和进程间消息传递等。

anst

四、应用组件

Android 每个应用包含四类组件：

  • Activities        与用户交互
  • Services         与应用有关的后台服务
  • Broadcast Receiver      Android 系统和应用的通信
  • Content Provider       与其他应用的通信

每一个Activity 对应着一块屏幕和一个与用户交互的事件，比如一个Android 邮件应用，有一个activity 是列出所有邮件，一个activity 读邮件，一个activity 写邮件等。所有的activities 都是源自于应用启动时的一个activity，类似于所有函数都是源于main() 函数调用。

一个Service 对应着一个后台持续运行的线程，比如一个后台播放音乐，在比如不中断用户操作的方式从网络上获取数据。

Broadcast Receiver用于回应其他应用或者系统广播的消息。比如一个应用可能发起广播给其他程序某些数据已经下载完毕了，那么Broadcast Receiver 则会截获这则消息并发起相应的动作。

Content Provider 通过请求用于向其他应用提供数据，例如第三方应用请求读取你的通信录。这类请求通过ContentResolver 类处理。一个Content Provider 可以连接多个Content Rsolver。他们关系如下图所示：

Android Training Bangalore

Android 还有其他一些组件，如Manifest 是应用的配置文件，Resources是外部元素，如变量和静态图片等。

五、文件组织结构

以Android Studio 为例，新建一个项目时，会在C:\Users\[your name]\AndroidStudioProjects 下创建你的项目对应的文件夹，而在Android Studio 视图中则有至少manifests、java 和res 三个目录。这三者分别保存配置文件，源代码和资源静态文件。

Screen Shot 2015-11-16 at 10.37.04 PM

  • manifests 目录下有AndroidManifests.xml 文件保存应用的配置信息，它告诉了系统需要哪些资源，以及如何构建起这个应用。
  • java 或src 目录下保存系统的 java 源文件
  • res 保存了用户交互所需要的资源，可能有子文件夹
    • drawable  保存图片
    • layout  保存屏幕布局
    • menu  保存屏幕菜单
    • values 保存为屏幕预定义的值

可能还可能有其他文件夹：

  • gen 是平台IDE 环境在编译时产生的中间文件
  • libs  外部的库文件

六、Android application package （APK） 生成过程

andriod的安装文件.apk如下图所示生成：

apk-structure

  1. .java源文件javac 编译为.class 二进制文件
  2. 项目.class 和其他外部库.class 通过dx编译为classes.dex 二进制可执行文件
  3. aapt 将classes.dex 二进制可执行文件、配置文件AndroidManifest.xml 和Resources 文件打包为apk 文件

知道了这个过程，那么你也可以通过将apk 反编译为xml、资源文件和源码等了。

 

 

 

存储系统中的纠删码（Erasure Codes）—有限域（三）

Posted on by
回复

有限域是纠删码中运算的基础域，所有的编解码和重建运算都是基于某个有限域的。在讲讲为什么纠删码不能基于一般常见的域（自然数域，实数域）之前，需要讲讲域的概念和有限域与其他域的区别。文章将以尽量简单的语言使得更多的读者能够看懂。

一、有限域的基本概念

1. 什么是域？

首先回顾下我们学习数学的历史：从刚开始接触数学时，我们首先学会一些符号（比如从1开始数到100，初中开始学习未知数x, y, z 等），接着开始学习基于这些符号的运算（加减乘除等），这些符号和运算就可以构成一个“域”。比如我们最早接触的是整数域，接着有理数域，然后在高中和大学还接触了虚数域，只不过当时老师没有告诉你这些是域而已。还有一些常见的数不构成域，比如自然数、素数、整数。

 

2. 域具有哪些性质？

在抽象代数中，域是一个非零的可交换环。在域上可以进行我们常见的加减乘除算法，一个域具有以下性质：

  • 加法和乘法的封闭性，加法和乘法结果还在域内
  • 加法和乘法的交换律；a + b = b + a  和  a · b = b · a.
  • 加法和乘法的分配律：a + (b + c) = (a + b) + c  和  a · (b · c) = (a · b) · c.
  • 加法和乘法的分配律：a · (b + c) = (a · b) + (a · c).
  • 存在加法和乘法的单位元素：a+0 = a 和 a·1 = 1（这里的0,1 不是自然数的0,1，代表着域上的加法单位元素和乘法单位元素）
  • 每个域上的元素都存在其负元和逆元： a+(-a) = 0, a·(a-1) = 1

这些性质和我们平时遇到的许多运算性质相同，这是因为我们很多运算就是在域上进行的。

继续阅读 →

存储系统中的纠删码（Erasure Codes）—XOR 码和RS 码（二）

Posted on by
2

纠删码（Erasure Codes）能够总体上分为XOR 码和RS 码两类，XOR 码基于有限域GF(2)，编、解码只需要按位异或（bit-wise exclusive-OR）即可完成，速度较快；RS 码基于有限域GF(2w)，编、解码需要有限域上（后面的文章将详细介绍）的运算，速度慢于XOR码。常见的XOR码有：

  • 低密度奇偶校验码（Low Density Parity Code, LDPC）
  • 柯西-里德所罗门码（Cauchy-Reed-Solomon Codes，CRS）
  • RAID码（如RAID5、RAID6）
  • 奇偶码（EVENODD）
  • X-码（X-code）

按照编码理论来说，RS码是一个字长为n，维度为k，码字间距为n-k+1 的最小距离可分码（MDS codes），但为了能够让读者能够更容易接受，我们这里的RS 码是基于有限域上GF(2w)编解码运算的编码。

继续阅读 →

存储系统中的纠删码（Erasure Codes）—综述（一）

Posted on by
回复

一、背景与挑战

数据的爆炸式增长使得存储系统的规模不断增加，存储设备的可靠性却一直没有得到显著提高（SSD 从SLC 到MLC 和TLC 可靠性不断下降，磁盘随着单位面积写入数据更多导致可靠性无法提升），从而给数据的持久化存储带来巨大挑战。另外随着存储系统规模的增大，存储系统中的冷数据的增加将远超过热数据的增加，如何安全保存冷数据，在需要的时候能够获取冷数据也成为存储系统中的重要挑战。下面是近年全球估计的数据量增长情况（GB,TB,PB,EB,ZB,YB…）。

2007    281 EB
2010     1.2 ZB
2011     1.8 ZB
2020      35 ZB

继续阅读 →