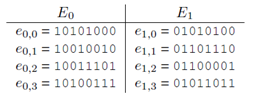Efficient Encoding Schedules for XOR-based Erasure codes
回复
求组合数、排列数等
最近写程序一直遇到组合数，排列数等问题。文章介绍程序实现全排列
、组合
中每个项的列举。
全排列 有顺序的排列n 个数；
组合 从n 个数中选取k 个进行无顺序的组合；
附：一般性的排列
可以通过组合和全排列一起完成。
减少分布式存储系统中基于异或(XOR)冗余编码的修复带宽
背景：分布式存储系统中越来越多地使用冗余编码减少存储开销，保证数据冗余。但存在的问题就是在一个节点发生失效时，需要从网络上的节点下载大量数据修复丢失的数据块，也称修复问题。基于异或（XOR）的冗余编码速度快，易于实现。本文选自FAST12 中Rethinking erasure codes for cloud file systems: Minimizing I/O for recovery and degraded reads ，介绍减少基于异或编码的修复带宽。
问题：通常的修复过程是下载等于原始数据量的数据块，解码得到原始数据，然后经历一个再编码的过程得到丢失的数据块，但这样往往浪费了一些下载的数据，如何为基于XOR 的冗余编码找到最优的修复数据块，使得修复带宽最小呢？
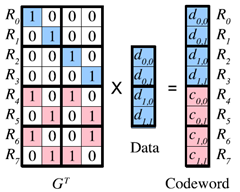
以生成矩阵（Generator Matrix）为下图的编码为例，如果丢失的第一个数据节点，相应地丢失了R0 和R1 对应的数据块，下载任意其他四块数据块可以修复这两块数据块，但显然不是最优的，最优的情况是下载R2、R4 和R7 所对应的数据块，就可以解码得到R0 和R1。
定义：
- F 表示为丢失的数据块对应行号的集合；
- {……} 表示相关数据块对应行号的一个最小集合，且有且仅有一个失效的数据块在其中。比如{R0，R2，R4} 满足R0 = R2 +R4，且R2 和R4 都不在F 中，以问题给出的图为例，这样的集合还有{R0，R3，R6} 等；
- {R0，R2，R4} 可以表示为10101000，其中对应的位上为1 表示该数据块在集合中；
- Ei 是所有{……} 中失效节点为i 的集合，即所有相关集合中包含i 的子集，按顺序写作ei,0，ei,1，……；
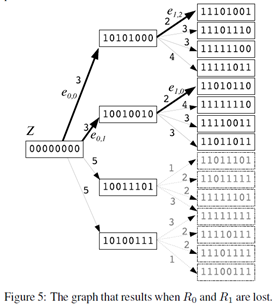
方法：构造一个有向图（如Figure 5），起点为全零的Z 串（00000000），边为Ei 中的元素ei,j ，边的权重为起点和终点的汉明距离，也就是需要的数据块的个数，每一层代表修复一个数据块。路径中权重最小的路径为最优修复路径（图中粗箭头所指）。
为构建该图，首先将F 中所有节点对应相关集合都计算出来，即E（ei,j 中i 表示节点，j 表示序号）：
以问题中的例子为例。从Z 开始，首先修复第一个数据块（R0），对应e 的权值为3,3,5,5，接着分别在已有的基础上修复第二个数据块（R1），并得到第二步的权值。使用Dijkstra 可得到最短路径，即最优修复数据块集合。
功能性修复再生码循环修复的一些性质
在我的开源的编码库中有一些判断功能性修复再生码（Regenerating Codes with Uncoded Repair）循环修复的一些性质，这里mark 一下。
前提：所有性质的判断都是针对通过随机线性码实现再生码的生成矩阵（generator matrix，GM），矩阵GM 有αn 行和c 列，相应的每个存储节点i 对应着矩阵GM 中连续的α 行，所以将每个节点的子矩阵（sub-GM）记作GMi 。每失效并修复一个节点时，相应的sub-GM 失效，并通过从d 个剩余sub-GMs 中获取dβ 个向量，随机线性组合为新的sub-GM。
TeXworks 快捷方式
以前一直用pspreview+xelatex+Notepad++，最近TeXlive2013 也试着安装了下，感觉TeXworks 的速度快，使用方便，有些特性非常实用。比如TeXworks 提供从pdf 源文件跳转到源码位置，只需要右键->跳至源文件，或者Ctrl+pdf上的位置，就可以跳转到源文件对应的位置了。TeXworks 有Preview window（显示pdf）和source window（显示源码）两个界面，在两个界面的快捷方式有：
d=k+1,n=2k,α=2,β=1 Exact Regenerating Code with uncoded repair— CME
文章bibtex
@article{陈勇2012基于组合矩阵的精确修复, title={基于组合矩阵的精确修复 MDS 编码< br/>}, author={陈勇 and 武国强 and 林宝军}, journal={宇航学报}, volume={33}, number={11}, pages={1654--1659}, year={2012} }
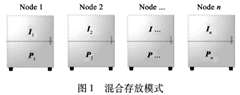
文章提出了d=k+1, n=2k, α=2, β=1 精确修复的再生码CME（Compound-Matrix Encoding），CME 是系统码，每个节点都保存了1/n 的原始数据，存放模式如下图，一半原始数据，一半冗余数据。文章在域GF(2) 下给出了详细的构造、修复方法。
