[翻译]原文:Genetic Algorithm for Solving Simple Mathematical Equality Problem
[翻译]地址:https://arxiv.org/ftp/arxiv/papers/1308/1308.4675.pdf
[翻译]目的:文章旨在为新手解释什么是遗传算法。并使用遗传算法这个工具一步步解决一个具体的数学问题——求解数学等式的解。
基本理念
在通过遗传算法寻找问题解的过程中,用染色体来表示一个解,一堆染色体叫做种群。染色体由基因构成,基因可以是数值的、符号的也可以是其他类型数据结构(视所解决的问题来定)。染色体通过环境适应度来衡量这个解对于问题的优劣程度。种群中的染色体通过交叉(交配)遗传到下一代,子代染色体是父代基因的组合。基因还会发生突变,遗传算法中使用交叉率和突变率来控制。
算法步骤
- 决定染色体数目、循环代数(决定遗传多少代)、突变率和交叉率;
- 产生染色体种群,并使用随机值初始化染色体中的基因
- 重复步骤4-8(重复次数等于循环代数)
- 考量每个染色体的适应值
- 染色体选取
- 交叉
- 变异
- 产生新的后代染色体
- 得到最终解
算术问题
以求解多元一次不等式 a+2b+3c+4d=30 为例,使用遗传算法找到a b c d 值满足该等式。很显然可以使用这样一个函数衡量适应度
f (x) = |(a + 2b + 3c + 4d) - 30|
a b c d 初始化为0到30之间的一个自然数。
步骤一 初始化 (下面步骤不完全和算法步骤对应)
随机生成六个染色体Chromosome[1-6]。
Chromosome[1] = [a;b;c;d] = [12; 5; 23; 8]
Chromosome[2] = [a;b;c;d] = [ 2; 21; 18; 3]
Chromosome[3] = [a;b;c;d] = [10; 4; 13; 14]
Chromosome[4] = [a;b;c;d] = [20; 1; 10; 6]
Chromosome[5] = [a;b;c;d] = [ 1; 4; 13; 19]
Chromosome[6] = [a;b;c;d] = [20; 5; 17; 1]
步骤二 评估
计算每个染色体的适应度。
F_obj[1] = Abs(( 12 + 2*05 + 3*23 + 4*08 ) - 30) = 93
F_obj[2] = Abs((02 + 2*21 + 3*18 + 4*03) - 30) = 80
F_obj[3] = Abs((10 + 2*04 + 3*13 + 4*14) - 30) = 83
F_obj[4] = Abs((20 + 2*01 + 3*10 + 4*06) - 30) = 46
F_obj[5] = Abs((01 + 2*04 + 3*13 + 4*19) - 30) = 94
F_obj[6] = Abs((20 + 2*05 + 3*17 + 4*01) - 30) = 55
步骤三 选择
适应度是越小越好,我们将适应度取倒数(加1避免出现除以0的错误),并归一化得到一个概率P
Fitness[1] = 1 / (1+F_obj[1]) = 1 / 94 = 0.0106
Fitness[2] = 1 / (1+F_obj[2]) = 1 / 81 = 0.0123
Fitness[3] = 1 / (1+F_obj[3]) = 1 / 84 = 0.0119
Fitness[4] = 1 / (1+F_obj[4]) = 1 / 47 = 0.0213
Fitness[5] = 1 / (1+F_obj[5]) = 1 / 95 = 0.0105
Fitness[6] = 1 / (1+F_obj[6]) = 1 / 56 = 0.0179
总计 Total = 0.0106 + 0.0123 + 0.0119 + 0.0213 + 0.0105 + 0.0179 = 0.0845
P[1] = 0.0106 / 0.0845 = 0.1254
P[2] = 0.0123 / 0.0845 = 0.1456
P[3] = 0.0119 / 0.0845 = 0.1408
P[4] = 0.0213 / 0.0845 = 0.2521
P[5] = 0.0105 / 0.0845 = 0.1243
P[6] = 0.0179 / 0.0845 = 0.2118
从结果可以看出基因4具有最高的适应度。接下来计算累计概率分布CPD:
C[1] = 0.1254
C[2] = 0.1254 + 0.1456 = 0.2710
C[3] = 0.1254 + 0.1456 + 0.1408 = 0.4118
C[4] = 0.1254 + 0.1456 + 0.1408 + 0.2521 = 0.6639
C[5] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243 = 0.7882
C[6] = 0.1254 + 0.1456 + 0.1408 + 0.2521 + 0.1243 + 0.2118 = 1.0
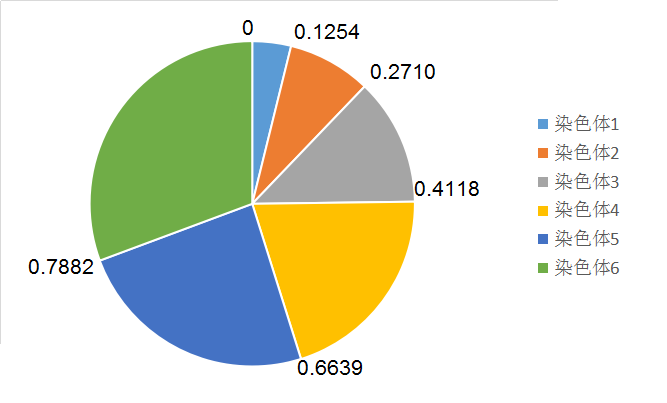
然后生成六个随机数R[i=1,2,3,4,5,6],通过这六个随机数在上图中的位置区间选择新的染色体,比如,当随机数在0.4118到0.6639之间则选择染色体4。不难看出,这种方法反应了适应度好的染色体具有更大概率被选择。
随机生成的六个随机数如果是:
R[1] = 0.201
R[2] = 0.284
R[3] = 0.099
R[4] = 0.822
R[5] = 0.398
R[6] = 0.501
那么相应的六个新的染色体是:
NewChromosome[1] = Chromosome[2] = [ 2; 21; 18; 3]
NewChromosome[2] = Chromosome[3] = [10; 4; 13; 14]
NewChromosome[3] = Chromosome[1] = [12; 5; 23; 8]
NewChromosome[4] = Chromosome[6] = [20; 5; 17; 1]
NewChromosome[5] = Chromosome[3] = [10; 4; 13; 14]
NewChromosome[6] = Chromosome[4] = [20; 1; 10; 6]
步骤四 交叉
假设交叉率为25%(0.25),那么生成6个随机数,如果随机数小于交叉数,则对应的染色体被选择用于交叉。比如随机数为:R[1] = 0.191, R[2] = 0.259, R[3] = 0.760, R[4] = 0.006, R[5] = 0.159,R[6] = 0.340。那么得到用于交叉的三对染色体是NewChromosome[1], NewChromosome[4] 和NewChromosome[5]。交叉方式为:
NewChromosome[1] >< NewChromosome[4]
NewChromosome[4] >< NewChromosome[5]
NewChromosome[5] >< NewChromosome[1]
下面决定从那个位置进行交叉。因为染色体长度为4,则随机生成1-(4-1) 大小的随机数,随机数用于表示基因从哪里开始交叉。
C[1] = 1 C[2] = 1 C[3] = 2
CrossChromosome[1] = [ 2; 21; 18; 3] >< [20; 5; 17; 1] = [ 2; 5; 17; 1] // C[1] = 1
CrossChromosome[2] = [20; 5; 17; 1] >< [10; 4; 13; 14] = [20; 4; 13; 14] // C[2] = 1
CrossChromosome[3] = [10; 4; 13; 14] >< [ 2; 21; 18; 3] = [10; 4; 18; 3] // C[3] = 2
那么剩余的种群中则有染色体:
NewChromosome[2] = [10; 4; 13; 14]
NewChromosome[3] = [12; 5; 23; 8]
NewChromosome[6] = [20; 1; 10; 6]
CrossChromosome[1] = [ 2; 5; 17; 1]
CrossChromosome[2] = [20; 4; 13; 14]
CrossChromosome[3] = [10; 4; 18; 3]
步骤五 突变
假设突变概率为10%(0.1)。考虑到6个染色体中每个有6个基因,那么将有4×6×0.1= 2.4 ≈ 2个基因发生突变,通过产生两个1-24范围的数值得到突变染色体位置(假设为12和18)。接着还产生两个1-30之间的随机数作为突变后的结果(假设为2 和 5)。那么得到新的种群如下(红色为突变基因):
Chromosome[1] = [10; 4; 13; 14]
Chromosome[2] = [12; 5; 23; 8]
Chromosome[3] = [20; 1; 10; 2]
Chromosome[4] = [ 2; 5; 17; 1]
Chromosome[5] = [20; 5; 13; 14]
Chromosome[6] = [10; 4; 18; 3]
步骤六 回到步骤二进行迭代
步骤七 至循环代数次结束
步骤六和步骤七类似,不再赘述。
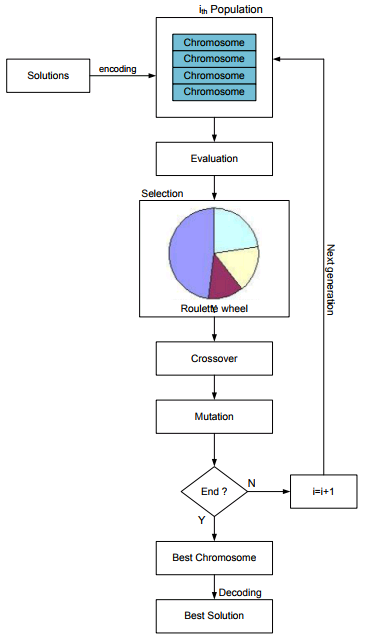
整个过程如下图所示:
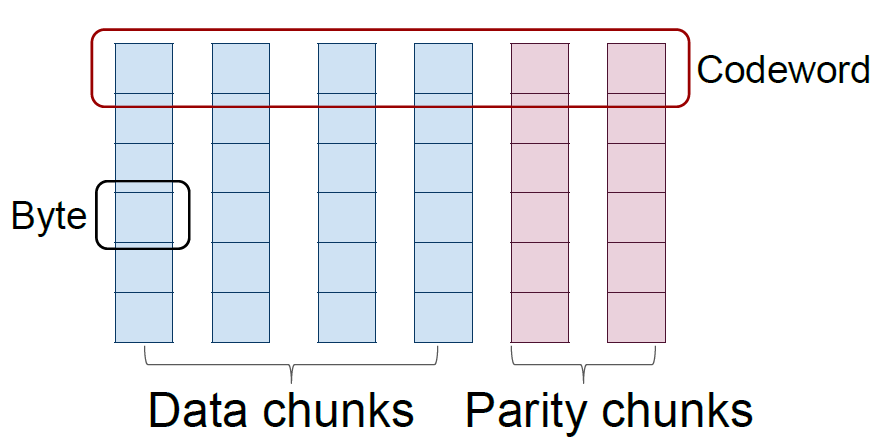
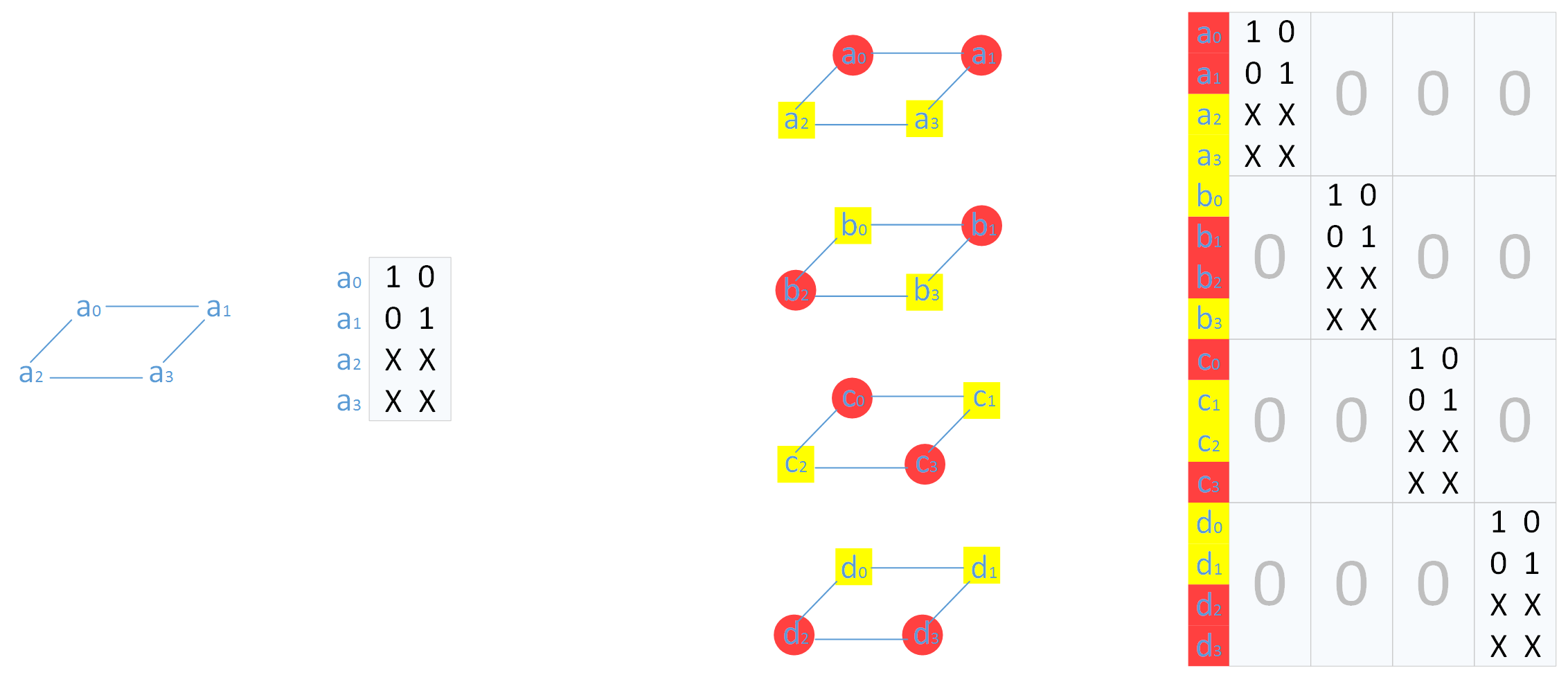
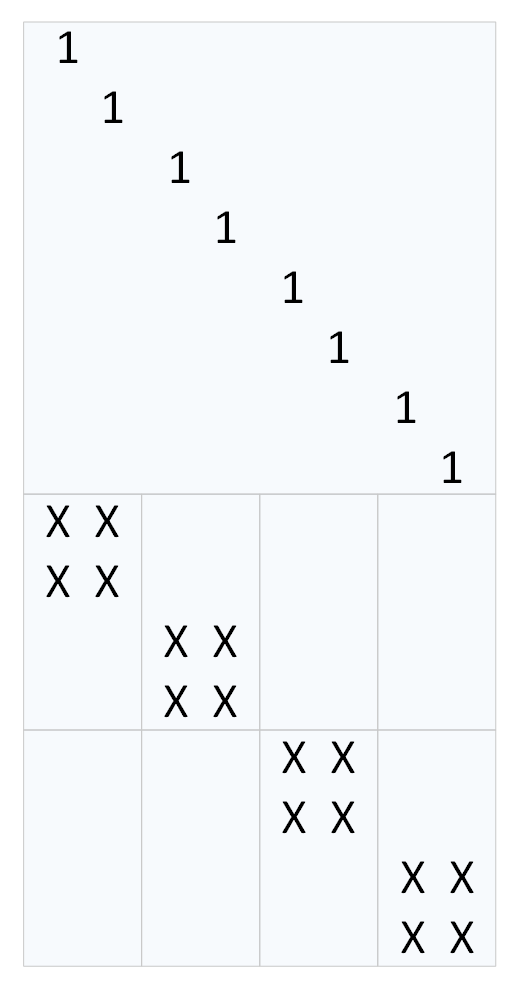
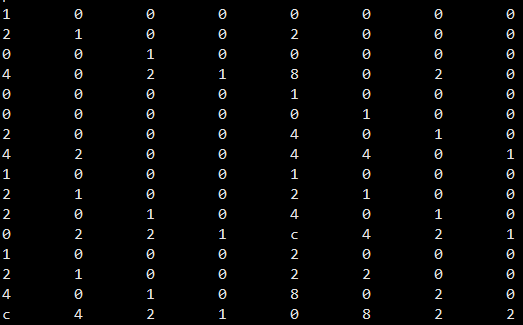
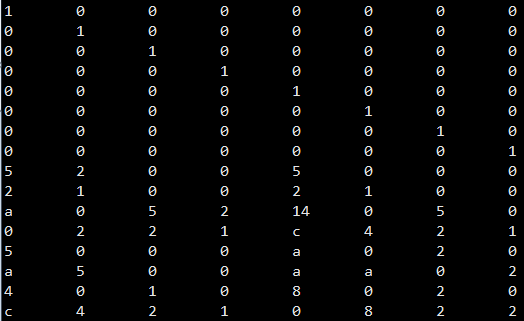
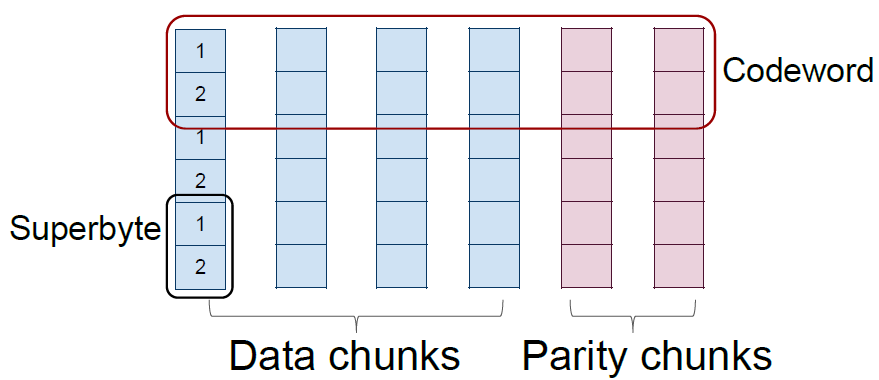 上图表示标量码,下图表示向量码。在磁盘阵列中,每个条带(stripe)也是横跨n 个节点,对应的一个码字,而码字中一个字节(标量码)或者超字节(向量码)则对应着条带中的一个数据块。一个(n,k) 标量码和向量码在生成矩阵中对应的是一个n×k 和nw×kw 矩阵,其中一个超字节包含w 个字节。
上图表示标量码,下图表示向量码。在磁盘阵列中,每个条带(stripe)也是横跨n 个节点,对应的一个码字,而码字中一个字节(标量码)或者超字节(向量码)则对应着条带中的一个数据块。一个(n,k) 标量码和向量码在生成矩阵中对应的是一个n×k 和nw×kw 矩阵,其中一个超字节包含w 个字节。
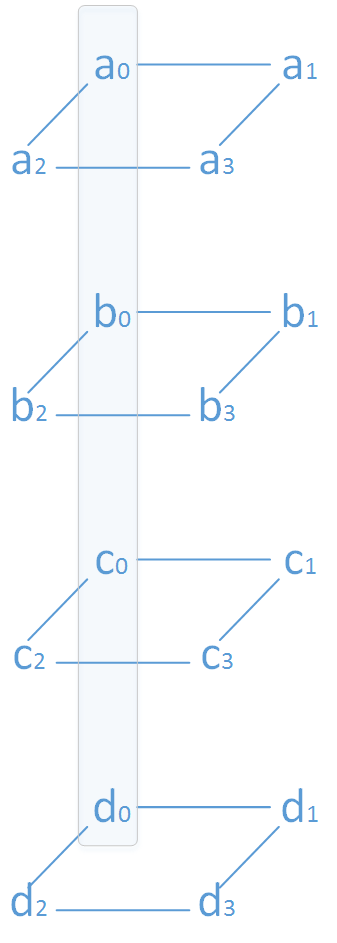
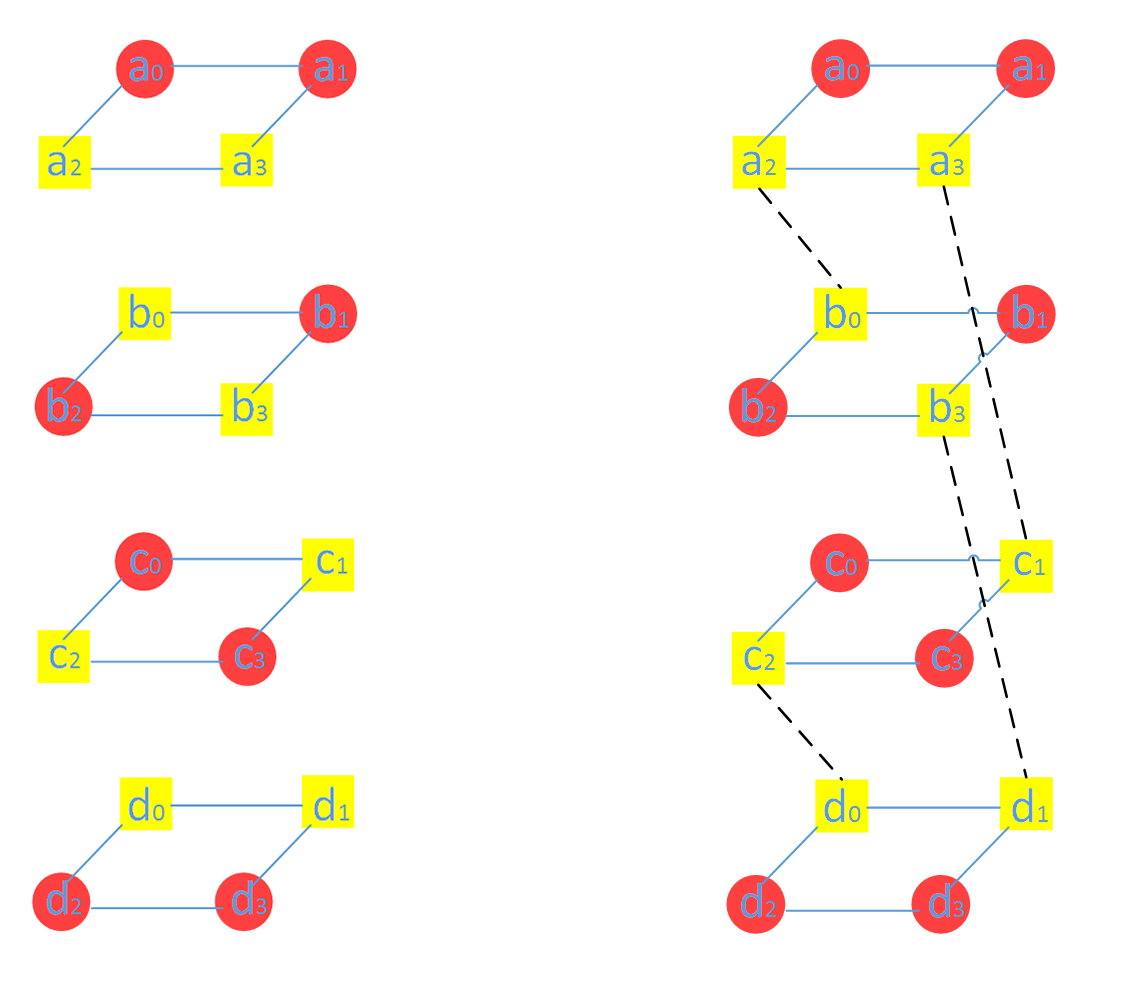
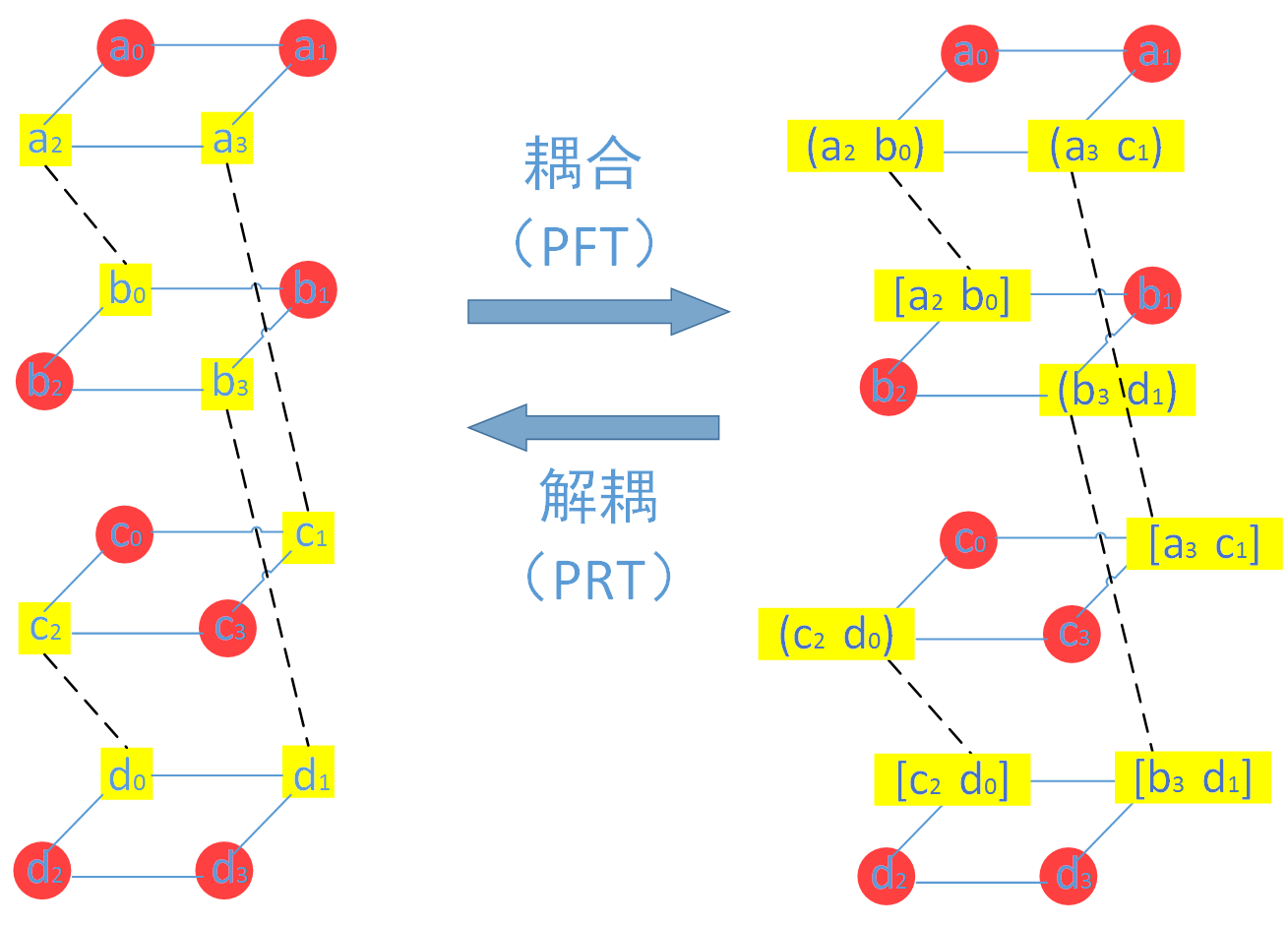
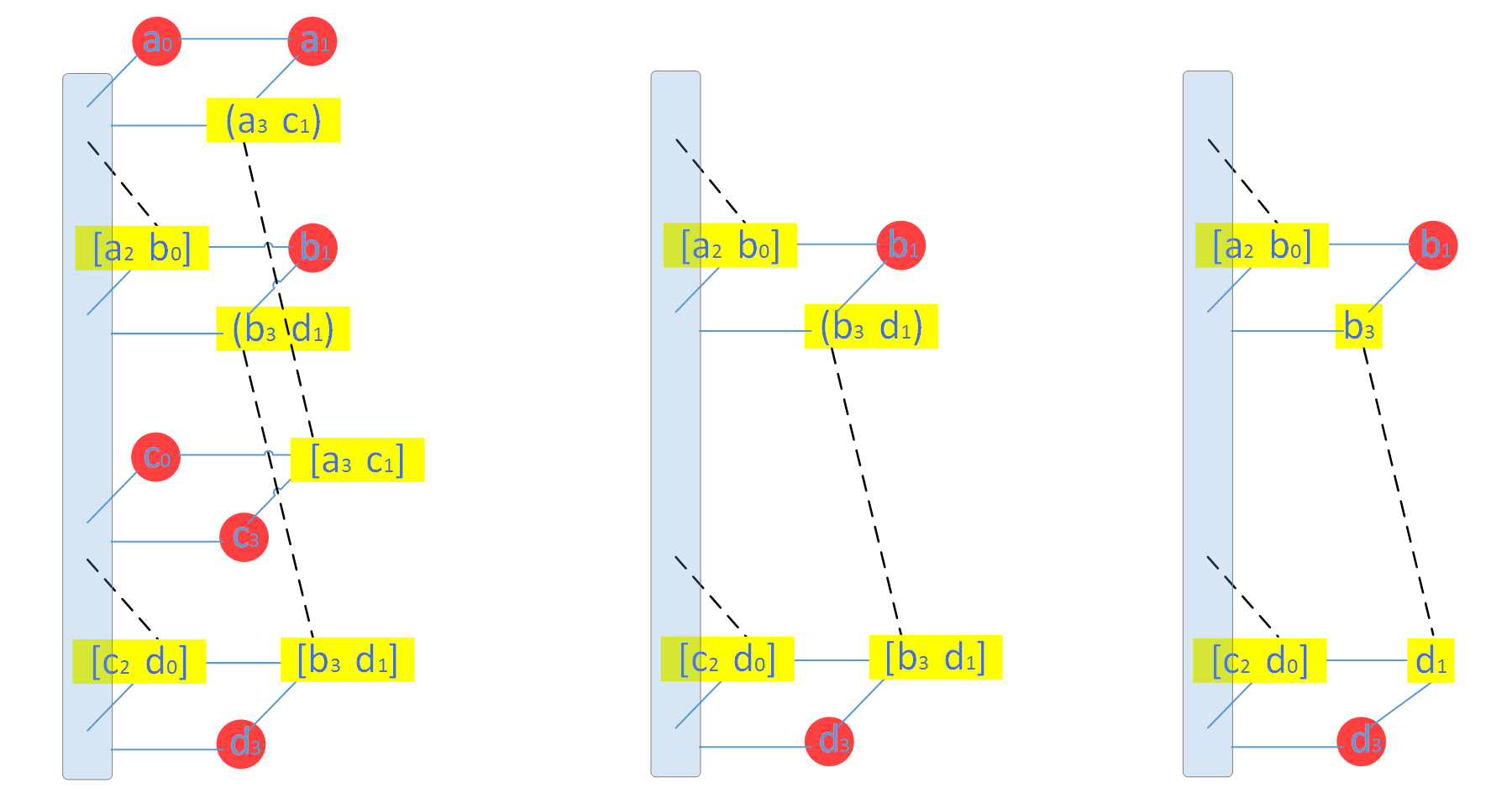
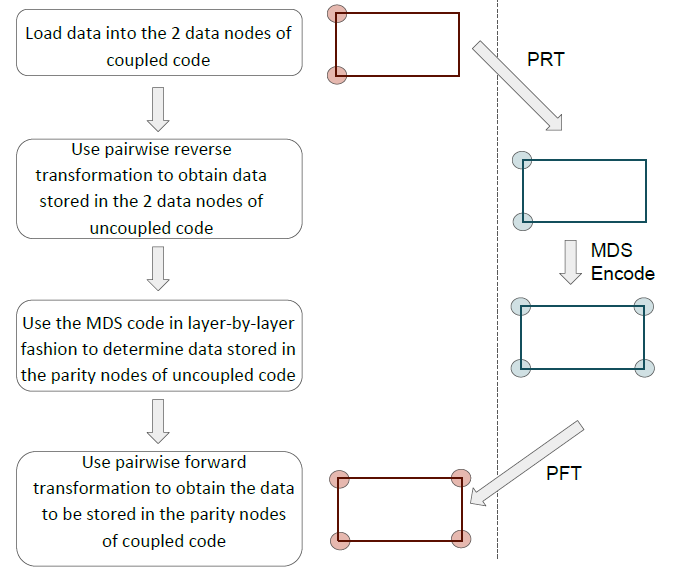 首先对原始数据进行耦合,经过MDS 编码后再解耦,这样原始数据还是原始数据,但校验数据不再是MDS 编码后的校验数据了。
首先对原始数据进行耦合,经过MDS 编码后再解耦,这样原始数据还是原始数据,但校验数据不再是MDS 编码后的校验数据了。