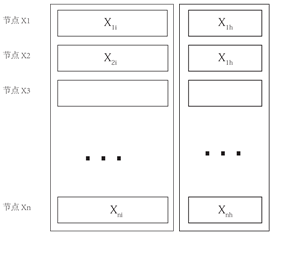
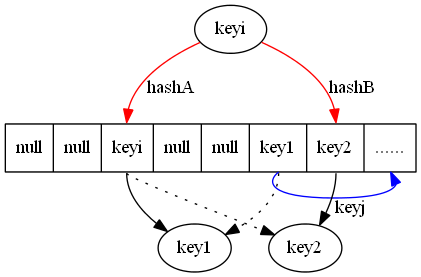
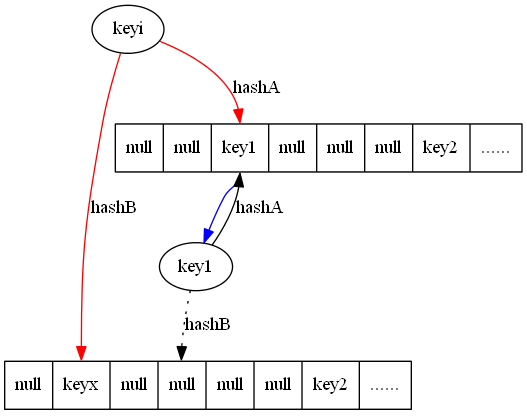
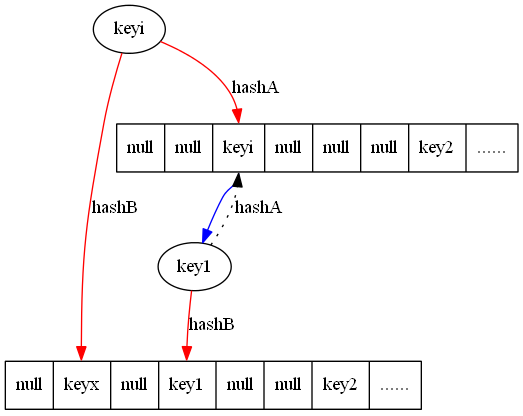
在传统的分布式存储系统中，数据为了保证安全、可靠、不丢失，一般采用副本策略，不使用编码技术有几点考虑：一是会增加了额外的计算开销；二是当某个存储节点发生失效时，会有多个存储节点涉及到该节点的恢复，且占用带宽超过副本策略的恢复带宽。下面是五种存储编码方法：
- Replication 副本策略（分布式文件系统hadoop 等采用）
优点：简单易实现，数据恢复带宽最小（C=1，C 什么意思看后面解释）
缺点：占用存储资源，现在云存储提供商都是按照存储容量来收费。
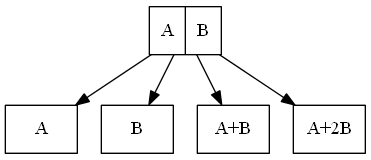
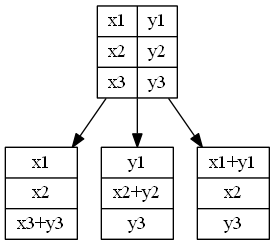
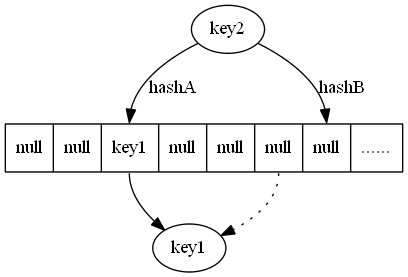
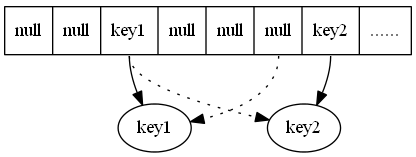
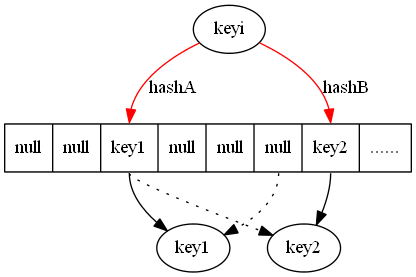
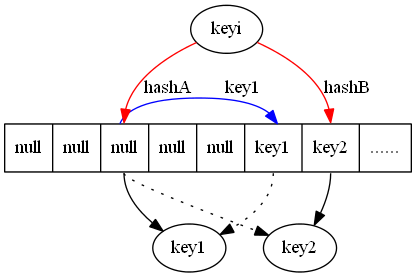
这里“+”代表的是按位加运算（0+0=0，1+0=1，1+1=0），简单策略允许至多两个节点失效，代价就是恢复需要额外的计算和两倍C=2 的恢复带宽。
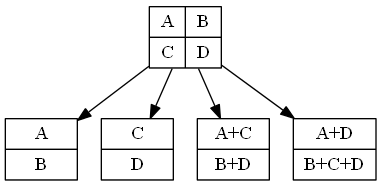
NCCloud 中改进了简单策略，在节点内部如果能够进行计算的情况下，恢复代价C 下降为1.5
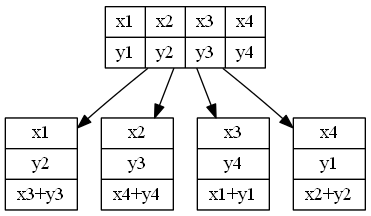
介绍一个参数向量，<N , T , C , A > 是用于衡量该编码方式应对存储节点失效的能力和效率：
- N =(单个节点存储容量)/(原始数据容量)，反映的是单个节点保存的信息占原始数据信息的比率。
- T 指最多可失效存储节点的个数。
- C =(恢复数据带宽)/(单个节点存储容量)，反映的是恢复单个失效节点的代价。
- A 指恢复单个节点涉及到的节点数。
|
名称
|
类别
|
码率 |
<N,T,C,A> |
总结 |
| replication |
[3,1] |
33.3% |
<1,2,1,1> |
副本，存储效率最低 |
| simple |
[4,2] |
50% |
<1/2,2,2,2> |
容错高，数据迁移大 |
| NCCloud |
[8,4] |
50% |
<1/2,2,2,2> 或 <1/2,2,3/2,2> |
内部允许计算时C 减小 |
| Infocomm |
[12,8] |
66.7% |
<3/8,1,2,2> |
再生编码 |
| RAID5 |
[3,2] |
66.7% |
<1/2,1,2,2> |
普通RAID
|
从编码的角度来看，[n,k] 码最多能检测发现n-k 个错误。同样的，k/n 指码率，即编码的效率，编码的效率越高，存储的效率也就越高，但如果要求存储效率高，那么能进行纠错的能力就弱。将数据通过编码保存在多个节点即将编码后的信息等长分片，分别保存在多个存储节点。这样每个节点保存了编码信息后的多个分片，如果一个存储节点保存的信息分片信息总量越多，节点失效后需要能够检测出的错误就必须越多，相应的n-k 就必须越大，码率越小。上面两种此消彼长的关系如下：
单个节点存储容量*允许失效节点<—>编码效率
存储利用率<—>编码效率
另外还需要重点谈到的是恢复带宽C 和恢复涉及的节点数目A ，当某个存储节点失效后，需要根据已有的节点上的数据恢复失效及诶单，恢复带宽大于或等于原节点存储容量，副本策略就是最优的带宽利用，只需要原始数据容量的带宽，特点策略的恢复带宽比较简单，但要计算出一般的普适规律也不是那么容易，首先来讨论恢复节点问题，我们希望恢复时所涉及到的节点越少越好，传统RAID 在这点表现的比较差劲，当一块盘发生故障时，进行该盘数据重建严重影响了其他磁盘对外服务，我们希望的情况是数据恢复、重建过程中涉及的节点越少越好。
考虑一种情况：将数据n 编码后等分为i 个分片存储，任意j 个分片参与至少可以恢复一个分片，那么任意j 个分片可恢复出整个数据n 。比如将数据a 分为a1/a2/a3/a3（i=4，j=2），任意一数据分片可以由其他两片恢复，那么如果a1+a2 恢复了a3，那么a1+a3 或者a2+a3 又可以恢复出下一个分片，这样所有的分片就都可以恢复出来，故有任意j 个分片具有数据n 的所有信息。（这里不考虑分区的情况，比如数据ab，都按照上面的分片方式，得a1/a2/a3/a3 和b1/b2/b3/b4（i=4，j=2），a 的分片和b 的分片都只能恢复各自的分片）这样根据需要恢复的节点数也可以得到存储效率小于或等于 j/i。比如副本策略j=1，i=3，存储效率 33%；简单策略j=2，i=4，存储效率 50%；infocomm 就出现了上面分区的现象，因为任意每个分片只需要两个分片就可以恢复，但是并不是任意的两个分片都能够恢复出一个分片。
接着考虑上面没有考虑到的第二种情况：任意一个分片可以由指定的j 个分片恢复，但是并不是任意两个分片就可以恢复出一个分片（与上面的不同的地方，这里更像RAID 一条strip 上只能互相恢复，与其他条带上数据无相关性）。其实这样每个条带上的各个数据分片还是满足上面任意j 个分片可以恢复出所有分片的要求的，i代表每个条带上数据分片数目，比如RAID5 j=i-1，RAID6 j=i-2，infocomm 策略 j=2，i=3。
存储节点保存一个或多个分片，分片和存储节点都可以是故障的单位，既可以是存储节点中的某个数据分片发生损坏，也有可能是整个存储节点失效。无论是上面第一种情况中的数据分片还是第二种情况中条带内数据分片必须分布在大于或等于j 存储节点。那么允许失效的节点最大即为所有节点数减去j。
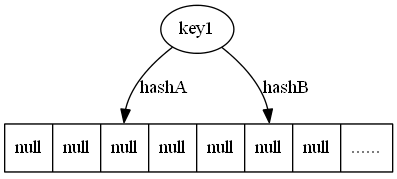
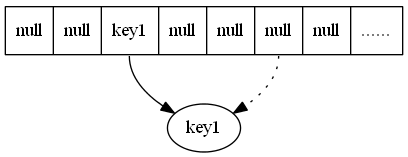
下面结束上面两种情况的话题，继续谈恢复带宽，我们发现给出的replication、simple、NCCloud、Infocomm、RAID 五种编码方法中除了replication 副本策略，恢复一个节点的代价C 都是大于等于二（例子里都等于二），这是因为恢复的数据分片都是通过其他数据异或运算得到的，异或运算最少需要两个参数，所以一个恢复一个分片至少需要两个分片，而节点是由数据分片组成的，所以恢复一个节点至少需要两倍的数据量。而副本策略存储的是数据的副本，恢复时不需要计算，节省了带宽。那么我们可以考虑每个存储节点上一部分分片采用副本策略，一部分使用异或运算提高存储效率。下面给出这样一种混合编码Hybrid。
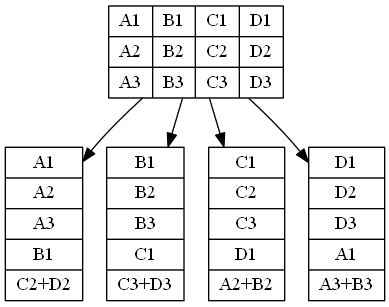
恢复每个节点的代价C 是8/5，存储效率是3/5，以恢复节点{A1/A2/A3/B1/C2+D2}为例：
A1 = A1
A2 = (A2+B2)+B2
A3 = (A3+B3)+B3
B1 = B1
C2+D2 = C2+D2
很明显，这样恢复代价C 越大，存储节点副本使用的就越少，恢复代价越大，也就是采用了更多的编码，恢复一个分片需要的分片数也就越多。恢复代价越小也就是存储节点内数据分片更多的采用了副本保存在其他节点，当存储节点恢复代价C=1 时，该节点上所有数据都在其他节点上保存有副本，这样存储效率也就<50%。
总结：存储效率等价于编码效率，反比于检错能力。恢复带宽正比于副本的使用，反比于异或编码比率。容最多节点反比于节点保存信息量，反比于编码效率和存储效率，即是码率越高，在节点保存信息一定的情况下，容失效节点越少。以上都是比较感性上的讨论，希望能够把信息论和编码的知识运用进去给出一个更加数学的结论。
是一个块可用的概率
是对B 的一个空间全划分，即包含了B 所有情况。这里的划分是将所有故障机器可能包含的分片（从0 到 n-m，如果超过n-m，那么可用的机器保存的分片少于m 个，也就无法恢复该块数据）。每一个
都代表着：当M 个故障机器中有i 个分片情况下，该事件（块可以被恢复）在所有可能情况下的概率。
