再生码(RC Regenerating Code)是07 年Infocomm 会议中Network Coding for Distributed Storage Systems 提到的一种分布式存储编码方式,相比RS 编码具有更小的恢复带宽,参考这里的分布式存储数据恢复问题。这笔记也是为了记录这篇文章。
分布式存储系统中为了保证数据的安全性,数据进行了的冗余编码,通过冗余编码使得数据块分散到各个节点上。这样存储环境的一个环境就是如何在节点失效,数据块(pieces)如何在这样的分布式环境中传递最少的数据来生成新的数据块。
Maximum-Distance Separable (简称 MDS) :系统码[n,k,d] 最小距离若为d=n-k+1,则称此码为极大最小距离可分码,指的是在这样的n 和k 的情况下,码字之间最小距离不可能大于d=n-k+1。如果码字之间所有的距离都是d=n-k+1,则这个编码是MDS。假设M bytes 的数据被分为n 个块,且其中至少任意k 个数据块可以恢复出一个原始数据。
Regenerating Codes (RC), which minimize amount of data that a newcomer must download subject to the restriction that we preserve the “symmetry” of MDS codes. At a high level, the RC scheme improves on OMMDS by having a newcomer store all the data that it downloads, rather than throwing some away.
原文中上面一段话讲出了RC 的设计思想(有别于数学,也有别于工程技巧),RC 让一个新来的用户尽量保存下从其他节点获得的数据,并尽量减少需要从节点下载的数据。
比较OMMDS(Optimally Maintained MDS)和RC 编码,当k=7 的时候一个新的节点在OMMDS 编码下需要向每个节点下载0.55M 数据,在RC 下向每个节点下载0.16M 数据。
文章做了一下几点工作:
- 引入了一个分析分布式存储系统中冗余方案的带宽需求框架;
- 总结了MDS 从其他节点恢复出新的MDS 数据块需要的最小带宽;
- 引入RC 再生码,通过仿真发现它比之前的编码方式需要维持更低的带宽。
比较前人工作,纠删编码方式比副本方式减少了一个数量级的带宽,但是在高扰动(high-churn)的环境下,纠删码带来更大的好处,但是带宽的代价对于p2p 存储系统来说却太大了。
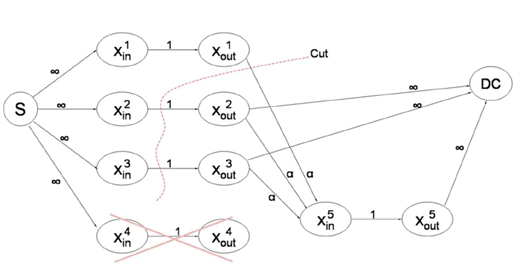
为了模拟分布式存储中节点以及编码存储方式和新节点加入的恢复,模拟了一个图G 包含存储原始数据S,用于获取数据DC 的数据收集器,和存储纠删码编码后存储数据块的Xin/out 节点,节点之间边表示链路,中间的数字表示边的权重,即是节点之间可以通过的最大流量。(这部分需要网络流的基础知识)如下图:
定义1:图G 中一个数据源S 和固定数据收集节点D 分割是一个全部边集合的子集C,使得从S 到DC 不存在可达的路径。最小分割指的是S、DC 之间使得所有边权重和最小的一个分割(后面最小割等同于最小割所有边的权重和)。
引理1:如果图G 中S 和DC 之间最小分割比初始对象大小还小,那么DC 无法恢复出原始数据。
证明:min-cut/max-flow(最小截断,最大流定理:从S 到DC 的最大流等于最小割),最小割小于对象大小,流也小于对象大小。从信息论的角度来看,不可能从比原始信息量更少的数据中恢复出原始信息。
命题1:假设在一些分布式存储方案中,我们构建图G ,内有n 个活跃的节点和![]() 个可能的DC,如果最小分割的最小值大于或者等于数据对象大小M,那么存在一个线性网络编码使得所有DC 都能够恢复数据。更进一步,随机网络编码通过增加域的大小,DC 可以以任意高的概率恢复出数据。
个可能的DC,如果最小分割的最小值大于或者等于数据对象大小M,那么存在一个线性网络编码使得所有DC 都能够恢复数据。更进一步,随机网络编码通过增加域的大小,DC 可以以任意高的概率恢复出数据。
证明:重建数据问题实际上等价于一个多播问题,一个数据源节点向所有的DC 发送数据。存在这样的线性网络编码满足min-cut/max-flow 限制。之前的工作也证明了通过增加域的大小,可将随机线性网络编码满足限制的概率提升任意高(有证明这种概率不小于![]() ,N 是G 中节点个数,d 是DC 的数量,q 是域大小)。
,N 是G 中节点个数,d 是DC 的数量,q 是域大小)。
命题2:假设数据被分为k 个块,通过(n,k)-MDS 编码每个编码后的数据块被存储在每个节点上。假设一个新节点通过在n-1 个活跃节点中下载每个块的a 比例的数据来重建新的数据块。那么![]() 。
。
证明:将信息流图G 视为存储系统。假设新节点和n-1 个节点交互,并从每个存储节点下载a 部分之个块。一个DC 和新节点与其他k-1 个其他存储节点交互,那么这个新形成的图中最小割如图所示为 k-1+(n-1-(k-1))a(DC 连接的k-1 个点的边和新节点连接的k 个点中没有和DC 相连的边),最小割=最大流所以应该等于k,所以 当![]() 时,可以重建出原始数据。
时,可以重建出原始数据。
注意到信息流图可以用来找到带宽需求,当新节点和k 个节点交互进行数据块重建时,不难证明新节点需要下载每个节点的完整数据块(这样对应的最小割为k-1+a)。对于(14,7) 纠删码,每个新节点只需要从n-1=13 个节点中下载1/7M 数据即可。我们把命题2的出来的最优MDS 称为OMMDS(Optimallyy Maintained MDS)。
============================= RC 再生码 ================================
RC 改进了OMMDS 存储下所有从其他节点获得的数据,因此具有更大的数据块,放大系数为![]() ,这样带来的坏处就是DC 需要下载更大的数据块了。然而当
,这样带来的坏处就是DC 需要下载更大的数据块了。然而当![]() 时,
时,![]() 。有码率
。有码率![]() ,重建数据块带宽开销为
,重建数据块带宽开销为![]() ,所以说MDS 在存储上有更好性能,但随着码率增大,带宽开销变大。
,所以说MDS 在存储上有更好性能,但随着码率增大,带宽开销变大。
定理1:假设所有存储节点存储aM bits数据,当一个新的节点连接k 个活跃节点并从每个节点下载了aM/k bits 数据,接着定义
![]()
,如果a<ac ,那么DC 从k 个存储节点中重建出数据理论上不可能的。当a大于或等于ac ,存在一种线性网络编码可重建数据,并且随机网络编码可以任意高概率重建数据。
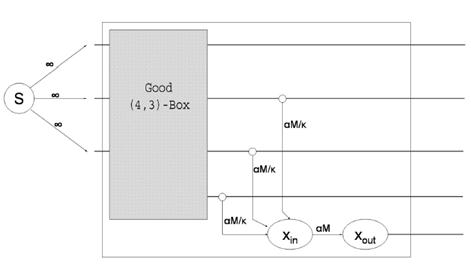
证明: 通过递归证明一个box 是一个good。box 是一个封闭的盒子,内部包含所有数据节点,输入是原始信息到数据块,输出是所有数据块块到DC 的连接,good 是指j 个输出中任意k 个端到端的流都可以重构出原始数据。当有一个新节点X 加入时,和上一层good 中k 个节点交互,边权重记做aM/k。需要满足包含新节点X 的这个box 也是一个good ,那么假设一个DC 和上一层good 中y1 个不参与重建新节点的数据块交互,并和y2 个参与重建新节点的数据块的数据块交互,y1+y2=k-1(剩余一个节点是新节点X ,不用考虑DC 没有连接新节点X 的情况,因为上一层good 满足任意k 个节点可以重建原始数据)。对应这样的图最小分割为:y1·a·M+y2·a·M+(k-y2)aM/k。满足最小分割大于M,即:y1·a·M+y2·a·M+(k-y2)aM/k >=M,最坏的情况下y1=0,得出
![]()
。
============================ 可靠性和维持带宽 ===============================
假设两个参数f 和a ,f 是单位时间失效节点的比例,a 是某个节点可用的概率。
副本:如果我们保存了文件的R 个副本,我们总共保存了R·M 的数据,单位时间修复带宽f·R·M ,文件不可用的概率为(1-a)R 。
理想纠删码:(n,k) 纠删码,创建一个新的数据块传输M/k 数据量(注:肯定大于M/k 的),设数据块数n=k·R,单位时间修复带宽f·R·M,不可靠概率为:![]()
混合:保存一个完整的副本和(n,k) 纠删码,编码数据块个数为n=k·(R-1),同样修复带宽为f·R·M,不可靠的概率为:(1-a)·Uideal
OMMDS:(n,k)OMMDS 编码共计RM 数据量,所有单位时间需要修复的数据为f·R·M。 但修复一个数据块需要额外![]() =(n-1)/(n-k) 倍的带宽,结果修复带宽为
=(n-1)/(n-k) 倍的带宽,结果修复带宽为![]() ,不可靠性和理想纠删码一样:
,不可靠性和理想纠删码一样:![]() 。
。
再生码:(n,k)再生码保存M·n·![]() 。因此修复带宽为f·M·n·
。因此修复带宽为f·M·n·![]() ,不可靠概率仍旧为理想纠删码不可靠概率
,不可靠概率仍旧为理想纠删码不可靠概率![]() 。
。
文章最后拿了四个trace 作比较,分析了在不同f 和不同数据安全性(数据可用程度)下的平均恢复聚合带宽。
Pingback引用通告: 再生码开销的定量计算 | 呆鸥