方法一:计算两点形成直线的斜率,斜率的负倒数是某点到该直线的斜率,通过计算垂足到该点距离得到某点到两点形成的直线距离。
方法二:矢量方法,好处是对于任意斜率都可以计算。
问题:已知点A (ax, ay),求到连接点B(bx, by) 和C(cx, cy) 的直线距离。
假设:建立坐标系,向量![]() ,
,![]() 和
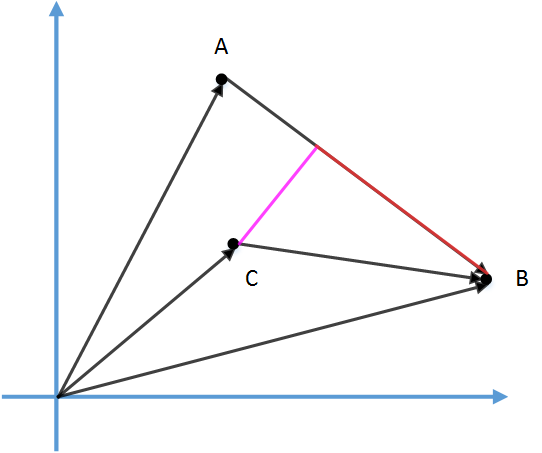
和![]() 分别对应三点的向量,如下图:
分别对应三点的向量,如下图:
图中C到直线AB 的垂线是紫色那根(假设垂足为D,图中未标注)。分别求得A 到B 的向量和C 到B的向量:
![]()
![]()
通过计算![]() 可以推导出红色线段长度为
可以推导出红色线段长度为![]() ,因为
,因为
![]()
再通过勾股定理得到垂线距离:
![]()
![]()