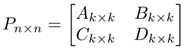文章bibtex

@article{陈勇2012基于组合矩阵的精确修复,
  title={基于组合矩阵的精确修复 MDS 编码< br/>},
  author={陈勇 and 武国强 and 林宝军},
  journal={宇航学报},
  volume={33},
  number={11},
  pages={1654--1659},
  year={2012}
}

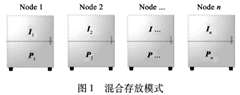
文章提出了d=k+1, n=2k, α=2, β=1 精确修复的再生码CME（Compound-Matrix Encoding），CME 是系统码，每个节点都保存了1/n 的原始数据，存放模式如下图，一半原始数据，一半冗余数据。文章在域GF(2) 下给出了详细的构造、修复方法。

一、CME 构造方法

既然CME 是系统码，那么生成矩阵GM 就由两部分组成，单位矩阵I 和冗余矩阵P（GM = [ I P ]^T）。冗余矩阵P 是一个2k×2k 大小矩阵，可以写成如下形式：

其中A_k×k = D_k×k，Bk×k = I_k×k – A_k×k，B_k×k = C_k×k。那么生成矩阵GM的构造方法就是冗余矩阵P的构造方法，知道了A_k×k 的构造方法也就知道了冗余矩阵P 的构造方法。

随机链式构造法构造A_k×k 的步骤如下：

步骤一：生成k×1 的全1 列向量ξ₁ ；

步骤二：随机将ξ₁  中某项置为0，记作ξ₂ ；

步骤三：查看列向量组中是否有k 个向量，如果有则跳至步骤五；否则继续；

步骤四：随机将新生成的矢量ξ_i 中某为1 的项置为0，记作ξ_i+1，然后返回步骤三；

步骤五：随机将生成的k 个列向量映射到A_k×k 的k 个列向量中；

接下来说明的是数据的放置方法：在B_k×k  和C_k×k 中依次找出最少0 项的那一列，如果该列第一个0 项元素在冗余矩阵的位置为(row, col)，如果对应row 行没有分配到节点，则将P 中第row 行编码的数据放在第col 个节点；否则继续找到该列下一个未分配的0 元素。

下面用一个例子来说明n=6，k=3，d=4，则构造出GM 如下所示：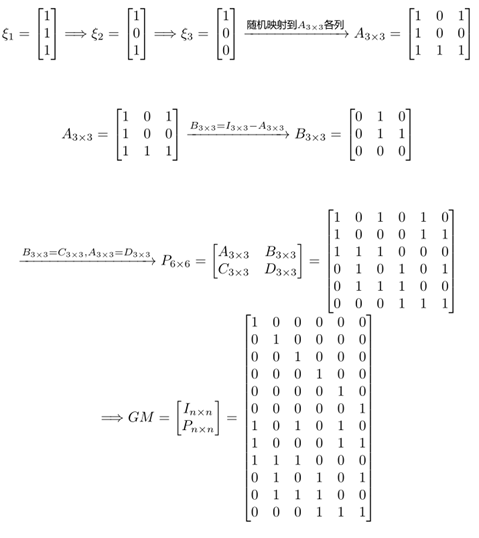

如果按照节点的顺序来排列生成矩阵GM，则GM 应该写成：

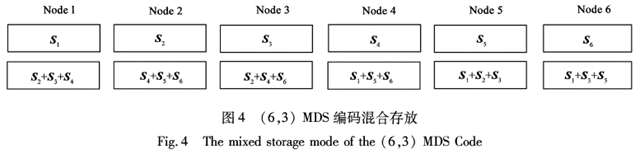
这样数据块的分布如下图：

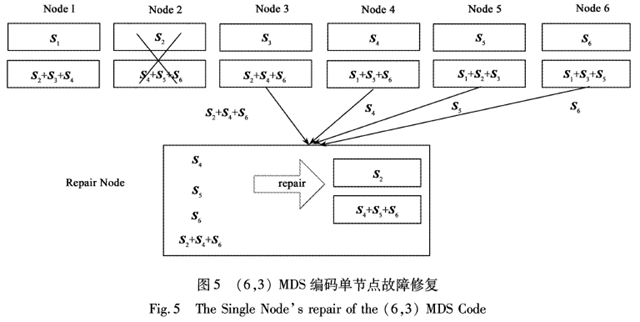
二、CME 修复方法

冗余矩阵有这样的特点：每行中有且仅有三个项为1，每个节点有且仅有4个列上有为1的项。

从GM 中不难看出每个节点最多只有d=4 列为1，那也一定在其他节点中包含这样的向量，其三个为1 的项和丢失的节点中四个为1的列中三个同列。那么只要下载这个向量和单位向量中的对应向量即可。

三、一些理论推导

命题一：采用如图1 的混合存储方式如果节点满足MDS 性质，则生成矩阵GM 中冗余矩阵P 每行至少有k 个非零项，且任意k 行线性无关，其中n=2k。

证明：任取k 行向量，这k 行向量一定在k 个节点的向量集合中，而由于MDS 性质，所以任意k 行向量线性无关。

不失一般性，取1到k k 个节点，则有rank[ I₁ , P₁ , …… I_k, P_k] = n = 2k，进而推导有rank[ I₁ , …… I_k, P_i] = k+1，P_i 为保证和任意k 个I_j 的不同组合满足上式，P₁ 至少需要k 个非零项。否则如果P₁ 有k-1 个非零项，则P₁ 可以表示为I₁ , …… I_k 中除去I₁ 后k-1 个向量的线性组合。■

推论：采用混合编码的存储系统，发生单节点故障时，当冗余矩阵P 每行有且仅有k 个非零项时，修复带宽取得极小值(k+1)M/n。

证明：（文章中的证明有些问题，没说明为什么修复I 和修复P 的系统数据块可以是一样的，下面是我自己的一些想法）考虑P₁,……,P_n 共计n 个行向量，每一行都是k 个I的线性组合，共计n×k 个I 组合成P₁,……,P_n ，那么I₁,……,I_n 每个I 出现k 次，这点可以反证，因为如果有I_x 出现了k+1次，假设包含I_x 的P 为P_{x,1},……,P_{x,k+1} ，那么P_{x,1},……,P_{x,k+1} 组成的向量组不是行满秩的。

这样，上面证明了每个I 在P 中出现的次数是一样的，即冗余矩阵P 中每列1 出现的个数是一样的，都是k 个。但是否能达成修复带宽取得极小值(k+1)M/n 是和P 每行的放置方法有关系的，比如下面的方式就不能保证修复带宽取得极小值(k+1)M/n：

完毕。

命题二：随机链式构造法生成的矢量组{ξ₁, ξ₂, ……,ξ_k }满足rank[ξ₁, ξ₂, ……, ξ_k] = k，且存在ξ_m = 1_k×1，1≤m≤k。

证明：根据链式构造规则，ξ₁ = 1_k×1 。ξ_i+1 和ξ_i 有且仅有一个项不同，那么ξ_i+1 – ξ_i =I_j  。由于ξ_i 有k 个项，这样对应线性无关的I_j 单位向量有k-1 个。因此，矢量组ξ₁，ξ₂ – ξ₁，……，ξ_k – ξ₁ 线性无关，即rank[ξ₁, ξ₂, ……,ξ_k] = k。■

命题三：按照之前方法构造的冗余矩阵Pn×n 任意行、列有且仅有k 个非零元素，且任意k 列线性无关。

证明：文中使用矩阵方式证明，其实在推论中已经证明了，就不再赘述。■

 

有一点文中没有介绍的就是为什么P 中行向量的分配是那样的以及链式构造向量的原因。而这些都影响修复时候1 个冗余数据块和k 个系统数据块的选择。

 

最后分析了下P 行向量分配的原则：选择B、C 中零元素放置到对应的行（B 对应的是4/5/6 行，C 对应的是1/2/3 行），则选择出来的行对应列是零元素，而对应I 在这列是1，比如下图中P(3,5) 的第三行放在第五个节点，第三行第五项为零，而第五个节点I 的第五项是1，避免了同个节点I 和P 有共同的列为1；

其次，A中是链式构造，那么总存在一行和另一行的汉明距离为1，AB构成k×n 大小的矩阵每一行都存在另一行和这一行汉明距离为2，选择B 中一列中0 项的行，那么通过该行所在节点的I 的作用（与对应的汉明距离为2 的行可以考虑作为修复时的冗余矩阵），使得修复可以完成。

最后的分析没有分析清楚，主要是对这个码的构造原理有待进一步考证。