一、特殊矩阵
正方矩阵/方阵( Square matrix ) 大小为n×n 的矩阵
单位矩阵( Identity matrix ) 对角线上元素为1,其余元素为0 的方阵,常用I 表示
置换矩阵( Exchange matrix ) 反对角线上元素为1,其余元素为0 的方阵,常用J 表示
对角矩阵( Diagonal matrix ) 非对角线上元素全为零的方阵
对称矩阵( Symmetric matrix ) 满足矩阵中元素eij = eji 的方阵
三角矩阵(Triangle matrix) 分为上三角矩阵(元素eii 以上元素为零)和下三角矩阵
正交矩阵(Orthgonal matrix) 满足MTM = I 的方阵,矩阵和矩阵转置的乘积为单位矩阵
二、有名的一些矩阵
1. Hadamard 矩阵
Hadamard 矩阵形式如下:
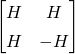
Walsh matrices作为hadamard 矩阵的一个特例,定义如下:
![]()
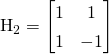
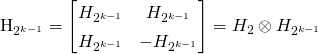
其中![]() 表示的是Kronecker product(kronecker 乘积)
表示的是Kronecker product(kronecker 乘积)
基本性质:
- kron(Hm, Hn) = Hm×n
- Hadmard 矩阵的行是正交的
- Hadmard 矩阵的任意行,或者任意列乘以-1 还是Hadmard 矩阵
- 对于所有矩阵A 行列式的值(det(A) < abs(Hn))都满足abs(A(i,j)) ≤ 1
2. Hankel 矩阵
Hankel 矩阵定义如下:
H(i, j) = H(i-1, j+1)
其形式如下:

基本性质:
- 对称的
- A+B 和 A-B 还是Hankel 矩阵
3. Hilbert 矩阵
Hilbert 矩阵定义如下(Hilbert matrix 是Hankel matrix 的一个特例):
H(i,j) = 1/(i+j-1)
下面是一个Hilbert 的例子:
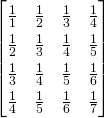
基本性质:
- 对称方阵
- Hilbert 矩阵的逆矩阵总是整数矩阵
- n×n 的Hilbert 矩阵
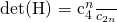 , 其中
, 其中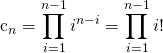
4. Vandermonde 矩阵
Vandermonde 矩阵定义如下:
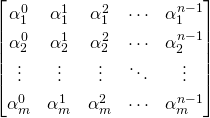
基本性质:
-
任意i (i<min(m,n)) 行满秩
-
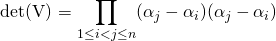
P.S. 写完以后发现我又闭门造车了,请读者参考这里吧: