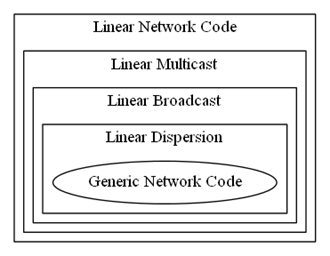
线性多播(Linear Multicast,LM)、线性广播(Linear Broadcast,LB)、线性扩散(Linear Dispersion,LD)、一般线性网络码(Generic Linear Network Code,GLNC)是网络编码理论中基础且容易混淆的概念。
在给出这四个概念的定义前先了解几个定义:
- < # > 表示的是向量集合# 生成的向量空间
- 对于节点T,VT = <{fd : d ∈ In(T)}> 表示节点T 所有输入链路的全局编码向量集合{fd: d ∈ In(T)} 所生成的向量空间
- 对于节点集合
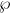 ,
,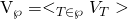 表示节点集合
表示节点集合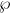 中节点所有输入链路的全局向量集合所生成的向量空间
中节点所有输入链路的全局向量集合所生成的向量空间 - 对于链路集合ξ ,Vξ = < fe : e ∈ ξ > 表示链路集合ξ 的全局编码向量集合所生成的向量空间
- maxflow(T) 表示信源节点S 到非信源节点T 的最大流
- maxflow{
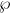 } 记做信源节点S 到非信源节点集合
} 记做信源节点S 到非信源节点集合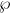 的最大流
的最大流 - maxflow{ξ} 记做信源节点S 到任意链路集合ξ 的最大流
- dim( & ) 表示向量空间的维度,如dim(VT) = 2 表示节点T 所有输入链路的全局编码向量集合所生成的向量空间的维度为2
有了上面的基础定义,我们看看线性多播/线性广播/线性扩散/一般线性网络码 的一般定义:
线性多播
在有向无环网络中,记列向量fd 为有限域F 上ω 维线性网络编码的全局编码向量,对于任何非信源节点T ,均存在由其所有输入链路d 的全局编码向量fd 的集合所生成的向量空间,记做VT = <{fd : d ∈ In(T)}> 。若对于每个满足maxflow(T) ≥ ω 的非信源节点T ,均有
dim(VT) = ω
此时的线性网络编码称为线性多播。
线性广播
在有向无环网络中,记列向量fd 为有限域F 上ω 维线性网络编码的全局编码向量,对于任何非信源节点T ,均存在由其所有输入链路d 的全局编码向量fd 的集合所生成的向量空间,记做VT = <{fd : d ∈ In(T)}> 。若对于每个的非信源节点T ,均有
dim(VT) = min{ω, maxflow(T)}
此时的线性网络编码称为线性广播。
线性扩散
在有向无环网络中,记列向量fd 为有限域F 上ω 维线性网络编码的全局编码向量,对于任何非信源节点T ,均存在由其所有输入链路d 的全局编码向量fd 的集合所生成的向量空间,记做VT = <{fd : d ∈ In(T)}> ,并记由非信源节点集合![]() 的全局编码向量集合构成的向量空间为
的全局编码向量集合构成的向量空间为![]() ,若对于每个的非信源节点集合
,若对于每个的非信源节点集合![]() ,均有
,均有
dim(![]() ) = min{ω, maxflow(
) = min{ω, maxflow(![]() )}
)}
此时的线性网络编码称为线性扩散。
一般线性网络码
有向无环网络中,记向量fd 和fe 为有限域F 上ω 维线性网络编码的全局编码向量,对于任意非空链路集合ξ = {e1 , e2 , … , em} ⊂ E,其中∀ei = Out(Ti),1 ≤ i ≤ m,m ≤ ω ,若
<fd : d ∈ In(Ti)> 不属于 <fe : e ∈ ξ\{ei} >
记做![]() ,则
,则![]() (记做fe ,e ∈ ξ)线性无关,则此时线性网络编码为一般线性网络编码。
(记做fe ,e ∈ ξ)线性无关,则此时线性网络编码为一般线性网络编码。
上面谈到的四个性质具有逐渐增强的关系,线性多播包含线性广播,包含线性扩散,包括一般线性网络编码,但反之不一定成立。
一般线性网络编码要求任何链路的集合内所有向量尽量满足线性无关性(min{ω, maxflow(ξ)} );当对任意链路放松要求,指定为任意节点的流入链路集合满足线性无关,则成为线性扩散;再对任意节点退化为单个非信源节点T ,则为线性广播;最后将单个节点约束为maxflow(T) ≥ ω 的非信源节点T收到所有信息(ω 个线性无关的)的要求,就是线性多播。
将上面这段话再分来来说:
线性多播:对于最大流大于或等于ω 的所有非信源节点,均可以收到信源节点发出的ω 个线性无关的消息。
线性广播:①. 对于最大流大于或等于ω 的所有非信源节点,均可以收到信源节点发出的ω 个线性无关的消息。②. 所有最大流小于ω 的非信源节点,均可以同时收到信源节点发出的部分消息,其信息总量等于该节点的最大流。收到ω 信息量表示收到了整个信息,线性广播表示一个非信源节点要么收到整个信息,要么收到最大流信息(每个进入链路向量都不相关)。
线性扩散:单个非信源节点和多个信源节点集合均满足广播性质。线性扩散表示一个非信源节点的集合要么收到了整个信息(ω),否则所有流入到这个集合的链路向量不相关。
一般线性网络码:对于任意非空链路集合ξ = {e1 , e2 , … , em} ⊂ E,若fe (e ∈ ξ)线性无关,则
dim( Vξ ) = |ξ | = min{ ω , maxflow(ξ) }
一般线性网络码则表示任意链路集合尽量满足线性无关性。
|
线性网络编码 |
定义 |
集合说明 |
|
线性多播 |
dim(VT) = ω |
针对满足maxflow(T) ≥ ω 的非信源节点T |
|
线性广播 |
dim(VT) = min{ ω, maxflow(T) } |
针对非信源节点T |
|
线性扩散 |
dim( |
针对非信源节点集合 |
|
一般线性网络码 |
dim( Vξ ) = |ξ | = min{ ω , maxflow(ξ) } |
针对链路集合 ξ |
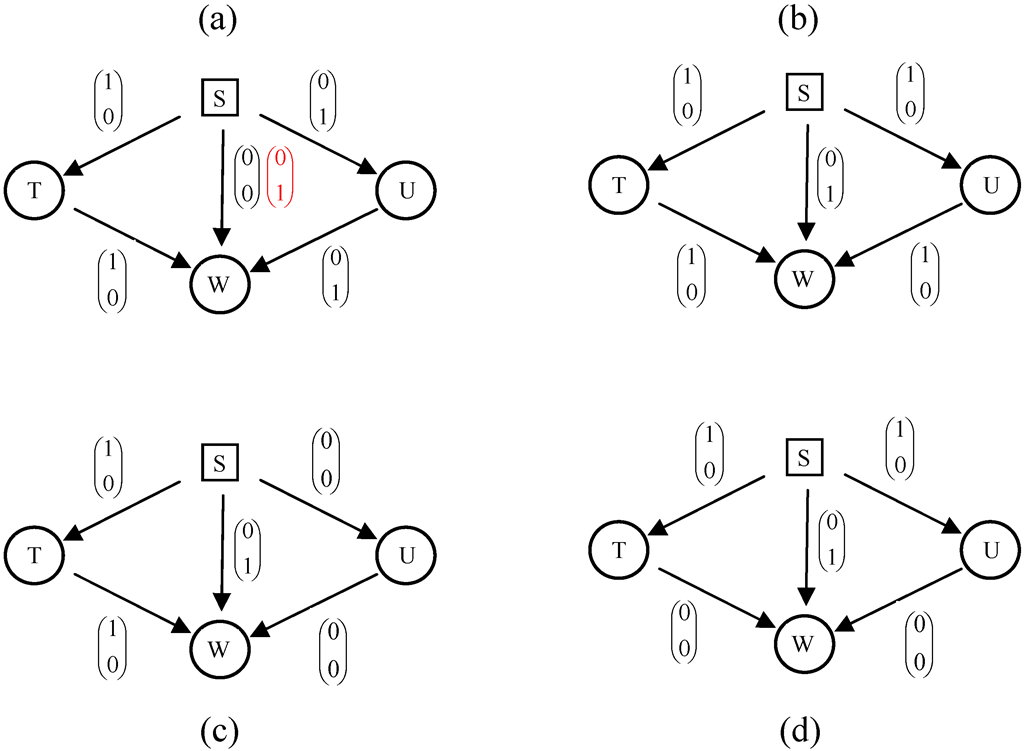
下面通过几个例子来说明线性网络编码、线性多播、线性广播、线性扩散和一般线性网络编码之间的包含关系:
(d) 线性网络码不是线性多播码:非源节点W 不满足线性多播性质。maxflow(W) > ω = 2 ,而dim(VW) = 1 ≠ ω
(c) 线性多播码不是线性广播码:节点都满足最大流大于2(只有节点W 满足)的dim(VW) = 2,是线性多播码。而非源节点U 的 dim(VU) = 0 ≠ min{ ω = 2, maxflow(U) = 1 } 的性质,所以不是线性多播码
(b) 线性广播码不是线性扩散码:非源节点E 都满足 dim(VE) = min{ ω , maxflow(E) } 的性质,是线性广播码。但是节点集合{T,U} 最大流maxflow({T,U}) = 2,ω = 2 ,而fST 和fSU 两个列向量线性相关,所以dim(V{T,U}) = 1,不是线性扩散码。
(a) 线性扩散码不是一般线性网络码:当fSW 为红色列向量,任意个非源节点(T,U,W)集合的流入链接向量都满足最大线性不相关性质,所以是线性扩散码。但是链路fSU 和fSW 链路向量相关(而maxflow(fSU 、fSW ) = 2,ω = 2),不满足一般线性网络码的性质。
(a) 线性扩散码也是一般线性网络码:当fSW 为黑色列向量。