之前的文章（http://blog.foool.net/2017/08/用遗传算法解决简单的数学等式问题/） 中介绍了过如何使用遗传算法解决数学等式问题，即寻找满足等式

(a + 2b + 3c + 4d) – 30 = 0

的一组解。适应函数确定后，影响算法好坏的主要依赖于交叉概率（crossover ratio），变异概率（mutation ratio）、初始基因组大小（即用于交叉变异的基因个数）和基因初始阈值。基因初始阈值指的是基因的取值范围，比如等式中变量a/b/c/d 的取值范围，我在实验中限定变量为大小不超过100 的整数。下面给出本文的几个结论。

一、遗传算法也可以用于寻找唯一解

之前的文章 中寻找的是四元一次等式的一个解，这个解的个数是无穷的，遗传算法能够找到一个解，但每次找到的解也不相同。但如果要用遗传算法解一个包含四个等式的四元一次方程组（唯一解）也是可行的，只是时间话的需要更长。比如遗传算法解四元一次等式平均需294 次迭代，解四元一次方程组需11400 次迭代（所有参数同之前的文章）。本文使用的四元一次方程组为：

(a + 2b + 3c + 4d) – 30 = 0

(2a + 2b + 2c + 2d) – 24 = 0

(3a + 1b + 7c + 1d) – 60 = 0

(4a + 3b + 2c + 1d) – 30 = 0

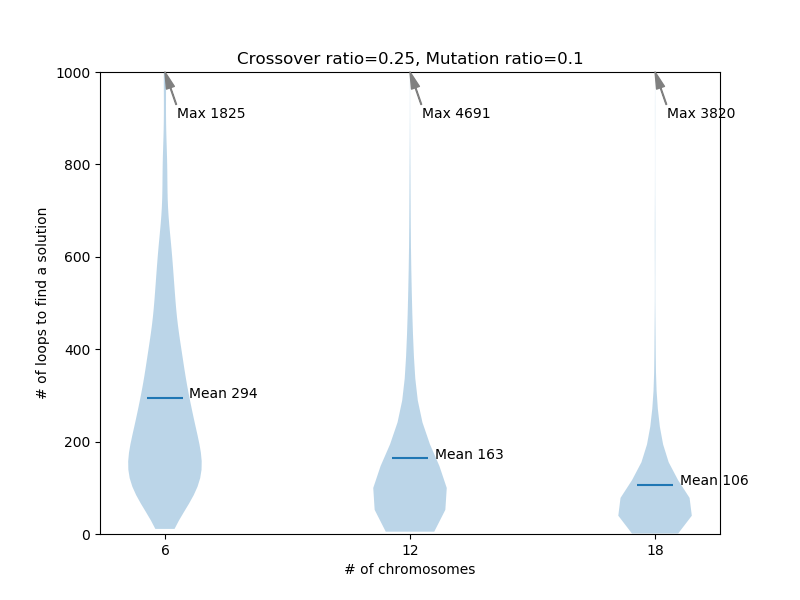
二、增加初始基因组大小有可能加速算法速度

增加基因组中基因数量，那么每次迭代/循环中的基因数量更多，可能出现解的概率增大。在以四元一次等式为例的实验中，增加基因组大小的确显著减少了迭代的次数，即使考虑了增加基因数目而带来的增量计算，算法仍减少了程序的整体运行时间。

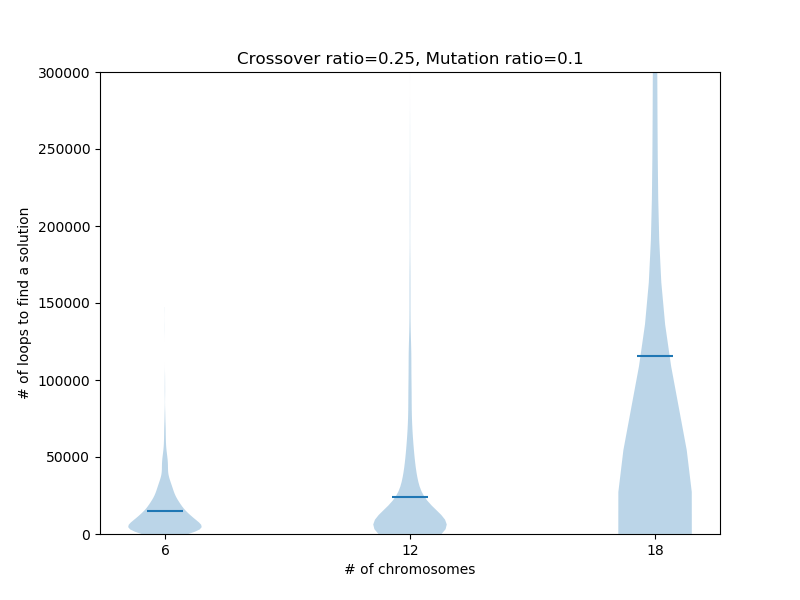
三、增加初始基因组大小也有可能不能加速算法速度

有点调皮了，这个结论是和第二点结论是相左的，如在其他参数相同情况下，随着基因组大小增大，遗传算法在解四元一次方程组需要迭代的次数增加。

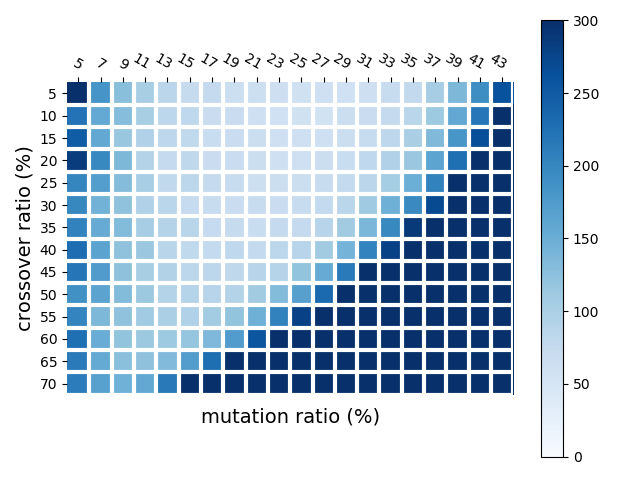
四、对于特定问题，参数大小影响算法性能大

下图是在基因组大小为18 时, 遗传算法1000 次测试四元一次等式求解所需要迭代次数的热力图，横坐标是变异率，从5% 到43%，纵坐标是交叉率，从5% 到70% 。热力图颜色范围是0-300，最深颜色表示300 次或300次以上迭代（比如在交叉率是70%，变异率是43%，实际迭代次数是9268次）。

综上，1.借助于适应函数，交叉、变异过程，遗传算法给出了一个在较大解空间快速求解的途径，但具体设计交叉、变异过程需要考虑特定问题；2.选取合适的参数极大影响了遗传算法性能，一般可以通过相似问题（复杂度更低）的参数选择作为参考（但是这种参考也不一定可靠，比如上面例子中，四元一次方程中增大基因组个数可以减少迭代次数，但在四元方程组中增加基因组个数却增加了迭代次数）。