文章来源:Erasure Coding vs. Replication: A Quatitative Comparison
再生码开销的定量计算
上篇论文讨论了再生码的来源:从OMMDS 改进而来,从理论上证明了再生码的可行性与存储开销,维持带宽。下面这篇文章:A practical study of regenerating codes for peer-to-peer backup systems 则详细讨论了再生码的存储开销、恢复带宽开销、计算开销等等。
冗余编码的存储系统中最多允许多少节点失效?
本文讨论分布式存储系统如果采用编码方式保存数据,那么允许最多失效的节点个数与码率之间的关系。这个关系也可以通过图论中“最小分割最大流”定理来求证。
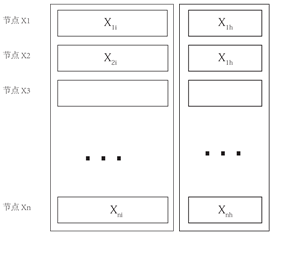
一个原始文件S(假设没有冗余信息)大小自信息量/文件大小为I ,进行冗余编码[n’,k](这里考虑系统码,为和分不到n 个节点区分开,用n’ 代替)的编码率为R = k/n’ ,则编码后文件大小为C:I → C = I/R。将编码后的数据分布在n 个节点上,每个节点的数据记做:X1 ,X2 ,X3 ……Xn ,每个节点数据的大小为C/n = I/R·n 。而每个节点数据/信息又有两部分组成,前一部分是系统码中的原始信息:Xii = I/n,另一部分是系统码中的校验信息:Xih = C/n – I/n ,且Xi = Xii + Xih。如下图所示
当a 个节点发生故障失效时,那么剩下的校验/冗余信息和原始信息应该能够恢复出丢失的原始信息,进而恢复出所有的校验信息。即:
![]()
因为H = C – I =I/R – I。得结果:
![]()
这也就是说,所有没有损坏节点的个数与所有节点比率(n-a/n)应该大于编码码率R。
再生码 Regenerating Code
再生码(RC Regenerating Code)是07 年Infocomm 会议中Network Coding for Distributed Storage Systems 提到的一种分布式存储编码方式,相比RS 编码具有更小的恢复带宽,参考这里的分布式存储数据恢复问题。这笔记也是为了记录这篇文章。
网关伪造ping 回应
环境:内网众多机器会发出ping,希望在网关上进行修改,使得所有ping 包在网关被截获,并返回ping reply。
最简单的解决方法就是iptables 转发的网关内部地址,由其负责回应ping。但这样就会使得ping 值非常小,作假也看着不像了。当时想写个程序控制回应ping 包,但这样回应就会有两个,一个网卡自身回应的ping 包,和程序回应的ping 包,为了拦截网卡本省发出的ping 包,可以采用内核模块编程,hook 住ICMP 包,这样有点超过我的范围了,调了一天多,放弃了。最后使用了一个折中的办法,iptables 将内网ping 包转发到外网ip 地址,运行ping 回应程序,最后iptables 拦截所有外网地址的ICMP 包,这样网关程序既可以收到ping 包回应,而外网卡的ping 被REJECT ,而内网卡的ping 不被REJECT。有个小小的问题就是client 收到ping 的回应都带有(DUP!),可能是因为报文的内容的原因,有知道原因的请告诉我哦~~~
再议SILT: A Memory-Efficient, High-Performance Key-Value Store
之前的文章谈到了高效key-value 存储系统SILT,谈的不清楚,昨天和付童鞋谈重复数据删除的时候谈到了SILT ,自己再回顾下。
首先要明白,SILT 融合传统的保存key-value 的三种方式:
- LogStore 以日志结构方式持久化存储key-value 对,内存保留所有key(来了请求就在内存key 中查找)
- HashStore 将磁盘或者SSD 上的每条key-value 按照内存中HashTable 的顺序排列,内存只保存了key 的部分哈希结构。
- SortedStore 按照key 的顺序对内存中原来HashTable 索引进行重新组织。SILT 使用的Tire tree。
HashStore 和SortedStore 都具有比较好的内存效率,但只读不可写。