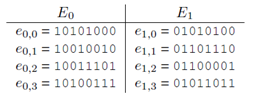分类目录归档:编码
减少分布式存储系统中基于异或(XOR)冗余编码的修复带宽
背景:分布式存储系统中越来越多地使用冗余编码减少存储开销,保证数据冗余。但存在的问题就是在一个节点发生失效时,需要从网络上的节点下载大量数据修复丢失的数据块,也称修复问题。基于异或(XOR)的冗余编码速度快,易于实现。本文选自FAST12 中Rethinking erasure codes for cloud file systems: Minimizing I/O for recovery and degraded reads ,介绍减少基于异或编码的修复带宽。
问题:通常的修复过程是下载等于原始数据量的数据块,解码得到原始数据,然后经历一个再编码的过程得到丢失的数据块,但这样往往浪费了一些下载的数据,如何为基于XOR 的冗余编码找到最优的修复数据块,使得修复带宽最小呢?
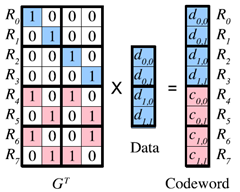
以生成矩阵(Generator Matrix)为下图的编码为例,如果丢失的第一个数据节点,相应地丢失了R0 和R1 对应的数据块,下载任意其他四块数据块可以修复这两块数据块,但显然不是最优的,最优的情况是下载R2、R4 和R7 所对应的数据块,就可以解码得到R0 和R1。
定义:
- F 表示为丢失的数据块对应行号的集合;
- {……} 表示相关数据块对应行号的一个最小集合,且有且仅有一个失效的数据块在其中。比如{R0,R2,R4} 满足R0 = R2 +R4,且R2 和R4 都不在F 中,以问题给出的图为例,这样的集合还有{R0,R3,R6} 等;
- {R0,R2,R4} 可以表示为10101000,其中对应的位上为1 表示该数据块在集合中;
- Ei 是所有{……} 中失效节点为i 的集合,即所有相关集合中包含i 的子集,按顺序写作ei,0,ei,1,……;
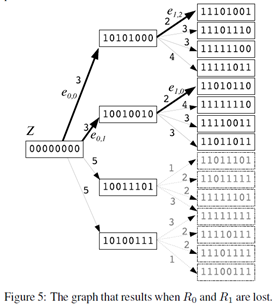
方法:构造一个有向图(如Figure 5),起点为全零的Z 串(00000000),边为Ei 中的元素ei,j ,边的权重为起点和终点的汉明距离,也就是需要的数据块的个数,每一层代表修复一个数据块。路径中权重最小的路径为最优修复路径(图中粗箭头所指)。
为构建该图,首先将F 中所有节点对应相关集合都计算出来,即E(ei,j 中i 表示节点,j 表示序号):
以问题中的例子为例。从Z 开始,首先修复第一个数据块(R0),对应e 的权值为3,3,5,5,接着分别在已有的基础上修复第二个数据块(R1),并得到第二步的权值。使用Dijkstra 可得到最短路径,即最优修复数据块集合。
功能性修复再生码循环修复的一些性质
在我的开源的编码库中有一些判断功能性修复再生码(Regenerating Codes with Uncoded Repair)循环修复的一些性质,这里mark 一下。
前提:所有性质的判断都是针对通过随机线性码实现再生码的生成矩阵(generator matrix,GM),矩阵GM 有αn 行和c 列,相应的每个存储节点i 对应着矩阵GM 中连续的α 行,所以将每个节点的子矩阵(sub-GM)记作GMi 。每失效并修复一个节点时,相应的sub-GM 失效,并通过从d 个剩余sub-GMs 中获取dβ 个向量,随机线性组合为新的sub-GM。
d=k+1,n=2k,α=2,β=1 Exact Regenerating Code with uncoded repair— CME
文章bibtex
@article{陈勇2012基于组合矩阵的精确修复, title={基于组合矩阵的精确修复 MDS 编码< br/>}, author={陈勇 and 武国强 and 林宝军}, journal={宇航学报}, volume={33}, number={11}, pages={1654--1659}, year={2012} }
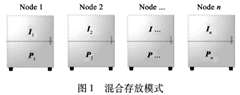
文章提出了d=k+1, n=2k, α=2, β=1 精确修复的再生码CME(Compound-Matrix Encoding),CME 是系统码,每个节点都保存了1/n 的原始数据,存放模式如下图,一半原始数据,一半冗余数据。文章在域GF(2) 下给出了详细的构造、修复方法。
最近收到推送的文章
这两个月收到不少scholar 推送的文章,有十几篇,抽空看看了。
1 Tree-Structured Parallel Regeneration for Multiple Data Losses in Distributed Storage Systems Based on Erasure Codes(基于纠删码的分布式存储系统中针对多数据失效的树型并行修复技术)
针对多块数据丢失再生冗余数据块进行了讨论,主要是优化速度,通过并行加速修复过程。提出了一种树型修复方式
2 An Improved Sub-Packetization Bound for Minimum Storage Regenerating Codes
文章讨论了MSR的系统码(systematic code)中B(文中用sub-packetization l表示)和k 和r=n-k 的关系。(n, k)-MSR系统码要求k不能太大,否则无法修复。文中虽然没有给出k 具体的上限,但给定了一个上限
3 Symmetry in Distributed Storage Systems
文章提出一种可以达到任意码率的精确修复的(n,k,d,,α,β)再生码方案:concatenation scheme
4 Impact of Stripe Unit Size on Performance and Endurance of SSD-Based RAID Arrays
文章讨论了SSD 中RAID 分片大小,4KB 条带更适合SSD RAID
5 RAIDq: A software-friendly, multiple-parity RAID
文章基于plank 和HP anvin 的文章提出了编解码速度非常快的RAIDq ,可以详细看看
6 Rateless codes and random walks for P2P resource discovery in grids
在P2P 存储系统中使用rateless codes 实现网络编码,较少资源更新时的网络开销
7 Efficient Encoding Schedules for XOR-based Erasure Codes
之前会议的文章的republish
8 Erasure coding for cloud storage systems: A survey
从MDS 到Regenerating codes 的survey,入门survey,讲的也不是很全,但普及了概念
9 Enabling Data Integrity Protection in Regenerating-Coding-Based Cloud Storage: Theory and Implementation (Supplementary File)
香港科技大学网络编码实验的一片关于NCCloud 和FMSR 的补充说明:加密和存储开销等
10 基于组合矩阵的精确修复MDS 编码
精确修复和GF(2) 是亮点,希望这篇不会让我失望