分类目录归档：存储系统

初探GF-Complete（伽罗瓦运算库）

Posted on by
回复

GF-Complete 是一个开源、综合性的伽罗瓦运算库，相应的文章发表在FAST13 中（见参考文献【1】）。作者是大名鼎鼎的Jim Plank 教授，作为开源纠错码库Jerasure 的开发者，在这个伽罗瓦运算库中创新地采用了SSE 指令集来加速纠错码运算的瓶颈—伽罗瓦运算中的乘法运算，并采用了其他运算方法，综合得到GF-Complete。该库可在Plank 主页中下载得到，下面就GF-Complete 库做简要分析，详细可参考文档【2】。

继续阅读 →

冗余编码的存储系统中最多允许多少节点失效？

Posted on by
回复

本文讨论分布式存储系统如果采用编码方式保存数据，那么允许最多失效的节点个数与码率之间的关系。这个关系也可以通过图论中“最小分割最大流”定理来求证。

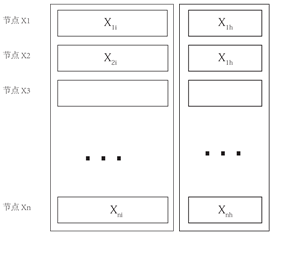
一个原始文件S（假设没有冗余信息）大小自信息量/文件大小为I ，进行冗余编码[n’,k]（这里考虑系统码，为和分不到n 个节点区分开，用n’ 代替）的编码率为R = k/n’ ，则编码后文件大小为C：I → C = I/R。将编码后的数据分布在n 个节点上，每个节点的数据记做：X1 ，X2 ，X3 ……Xn ，每个节点数据的大小为C/n = I/R·n 。而每个节点数据/信息又有两部分组成，前一部分是系统码中的原始信息：Xii = I/n，另一部分是系统码中的校验信息：Xih = C/n – I/n ，且Xi = Xii + Xih。如下图所示

6_0               6

当a 个节点发生故障失效时，那么剩下的校验/冗余信息和原始信息应该能够恢复出丢失的原始信息，进而恢复出所有的校验信息。即：

    $$\frac{n-a}{n} \cdot H \geq \frac{a}{n} \cdot I$$

  因为H = C – I =I/R – I。得结果：

    $$\frac{n-a}{n} \geq R $$

这也就是说，所有没有损坏节点的个数与所有节点比率（n-a/n）应该大于编码码率R。