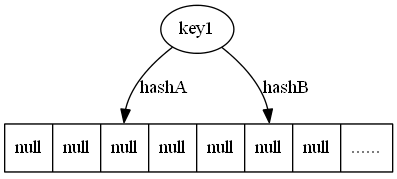
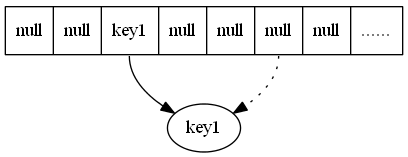
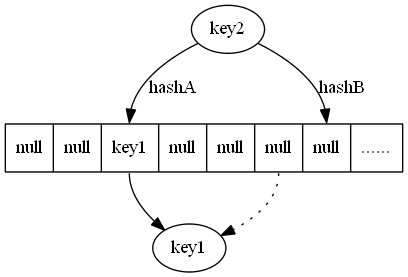
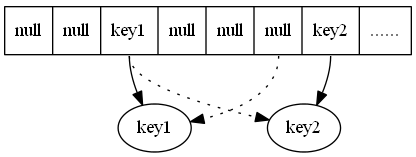
“单下划线”“_”开始的成员为保护成员,只有类对象和子类对象可以访问到这些变量/方法。
“双下划线”“__”开始的是私有成员,只有类对象能够访问,子类对象都不可以访问。
“from xxx import ”不可以导入“_”开始的变量/方法
私有变量/方法在代码生成前会被转化成为长格式(变为保护类型),转换机制为:变量/方法前加上类名,再将前端加上下划线字符。
比如A 类中有方法和变量 __private 会在代码解释前替换为 _A__private(类似于C 中的宏替换)
上面的如果明白了,可以到这里测试下。
“__xxxx__”这类双下划线开始,双下划线结束的变量为python 特殊变量,常见的有“__name__”“__file__”“__loader__”“__package__”。如果一个文件是作为主程序调用的,其值就会设为__main__,如果是作为模块被其他文件导入,它的值就是其文件名,常可用于模块内置测试。在python 的官方文档中有这样的解释:
The special global variables __name__, __file__, __loader__ and __package__are set in the globals dictionary before the module code is executed (Note that this is a minimal set of variables – other variables may be set implicitly as an interpreter implementation detail).
__name__ is set to run_name if this optional argument is not None, to mod_name + '.__main__' if the named module is a package and to the mod_nameargument otherwise.
__file__ is set to the name provided by the module loader. If the loader does not make filename information available, this variable is set to None.
__loader__ is set to the PEP 302module loader used to retrieve the code for the module (This loader may be a wrapper around the standard import mechanism).
__package__ is set to mod_name if the named module is a package and to mod_name.rpartition('.')[0]otherwise.
If the argument alter_sys is supplied and evaluates to True, then sys.argv[0] is updated with the value of __file__and sys.modules[__name__] is updated with a temporary module object for the module being executed. Both sys.argv[0] andsys.modules[__name__] are restored to their original values before the function returns.