参考：

[1] Finding the most fault-tolerant flat XOR-based erasure codes for storage systems [PDF]

[2] Determining fault tolerance of XOR-based erasure codes efficiently [PDF]

本文内容主要来源于上面两篇文章，主要讨论暴力搜寻方法具有最大容错能力（most fault-tolerant）的扁平（Flat）XOR 码。

XOR 码是通过异或运算（exclusive OR）进行数据编码、解码和重建的编码方法，其生成矩阵可以用1/0 二进制矩阵表示。

扁平码是一种每个节点只保存一个符号（数据块），即生成矩阵的每一行（列）对应一个节点。k 和m 分别表示原始数据块个数和校验块个数的话，扁平码的生成矩阵是一个(k+m)×k 大小的0/1 矩阵。常见的RS 码是扁平码，但不是XOR 码；CRS 码不是扁平码，是XOR 码。

暴力搜索通过遍历所有的解空间（所有可能的(k, m) 编码），通过计算每个解的性质，找到满足条件的编码。一个(k+m)×k 大小的0/1 矩阵有2^((m+k)×k) 种可能的二进制矩阵，如果将编码限制在系统码中，则有2^(m×k) 种可能的二进制矩阵。

[2] 中介绍了一种ME （Minimal Erasures）算法，是暴力搜索的关键，该算法通过找到最小失效列表（Minimal Erasure List）寻找某种编码的最大容错能力。ME 算法会用到几个术语：

汉明距离（Hamming distance）：如果一个编码的汉明矩阵是d，那么它能容忍的最大失效节点少于d 个。

失效样式（Erasure pattern）：一组失效（的数据块）使得有一个原始数据块无法被恢复。

失效列表（Erasure list）：所有失效样式的集合。

失效矢量（Erasure vector）：长度为m 的矢量，其中第i 个元素是失效列表中长度为i 的失效样式个数的总和。比如 < 0, 0, 3, 7, …> 表示有失效列表中有3 个长度为3 的失效样式，有7 个长度为4 的失效样式。失效矢量中第d 个值是第一个非零值（小于d 的失效均可恢复）。

最小失效（Minimal Erasure，ME）是一种特殊的失效样式，它的每个失效元素都是必须的，如果去掉其中之一，它就不再是失效样式。

最小失效列表（Minimal Erausre List，MEL）是一个编码的所有最小失效的集合。

最小失效矢量（Minimal Erasure Vector，MEV）是一个长度为m 的矢量，其第i 个元素是MEL 中长度为i 的ME 的个数。

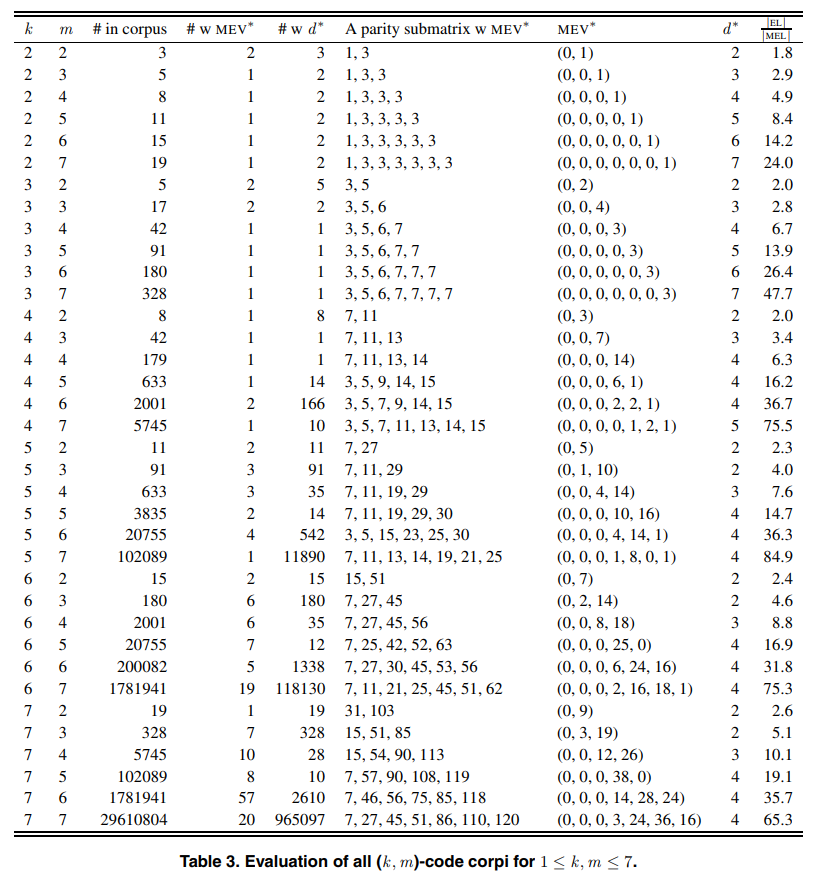
ME 算法具体详见[2] ，其输入是编码的生成矩阵（或Tanner 图），输出为MEL 和MEV。下图给出了 m < 8 和 k < 8 的结果。

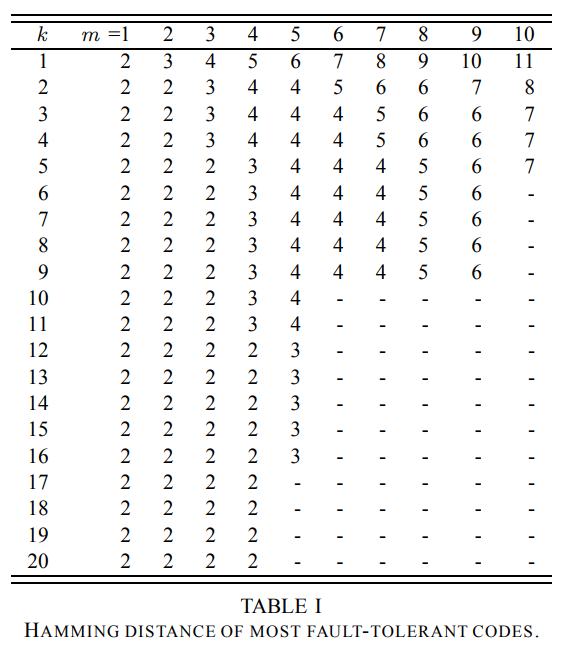
下图是m < 11 和 k < 21 所有扁平XOR 码的最大汉明距离。

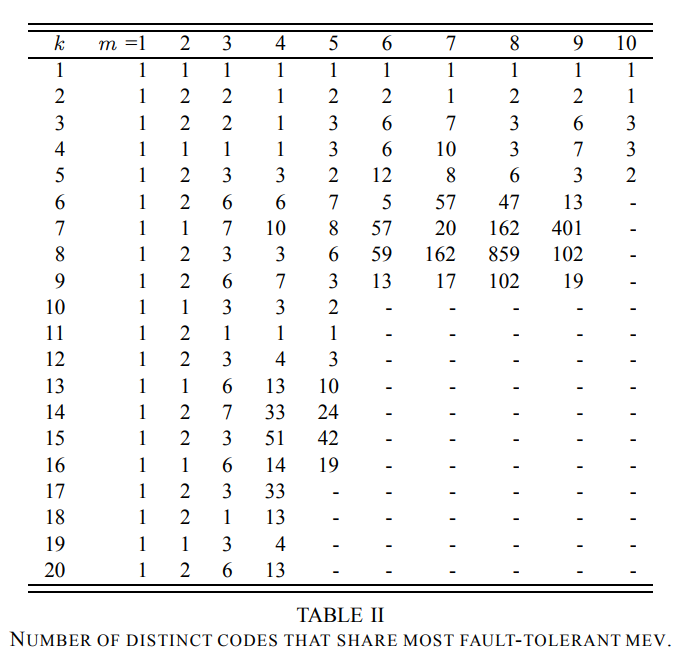
下图是m < 11 和 k < 21 所有扁平XOR 码中具有最优容错的个数。

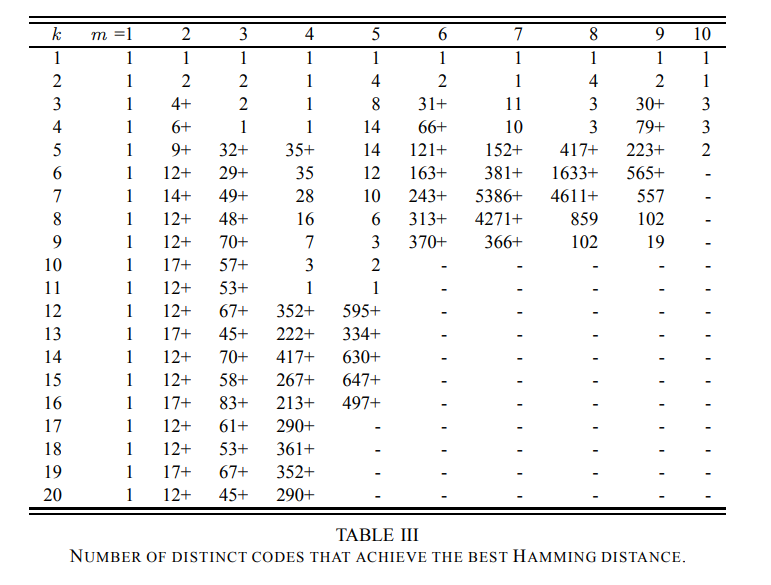
下图是下图是m < 11 和 k < 21 所有扁平XOR 码中能够达到最大汉明距离的个数。

[1] 还介绍了如何减少搜索的解空间等优化的方法，并指出搜索算法有部分是Python 写的，用C 能够进一步提高运算速度，并增加m 和k 的值。