问题来源：需要判断一个长度为N 的0/1 二进制字符串是自循环的概率是多少？自循环指的是一个字符串循环移位s 位仍然可以得到其本身，s 小于字符串长度。比如，010010 是自循环的，因为将这个字符串循环右移三个bits 字符串还是其本身。

通过自循环字符串特征很容易推导出：自循环字符串是周期性字符串，即字符串完全由若干个相同子串拼接得到，上面例子中重复的子串是 010。并且，自循环字符串移位得到其本身需要的最少步数s 和最小子串长度相同，也就是说，计算得到字符串最小重复子串也就得到了其自循环需要移位数s。

那么问题归结为如何找到一个周期性字符串的最小重复子串？

算法：令周期性字符串为S，那么SS 是两个S 的拼接，从SS 第二个字符开始，利用字符串匹配寻找S，如果SS 从第c 个字符开始包含了S 字符串，则S 的最小周期子串长度为c。下面是两个例子：

例子一：S =  010010

SS = 010010010010

1.  0 1 0 0 1 0 0 1 0 0 1 0  不是S
2.  0 1 0 0 1 0 0 1 0 0 1 0  不是S
3.  0 1 0 0 1 0 0 1 0 0 1 0  是S

结束，最小子串长度为3，即010 。

例子二：S =  abaaabaaabaa

SS = abaaabaaabaaabaaabaaabaa

1.   a b a a a b a a a b a a a b a a a b a a a b a a
2.   a b a a a b a a a b a a a b a a a b a a a b a a
3.   a b a a a b a a a b a a a b a a a b a a a b a a
4.   a b a a a b a a a b a a a b a a a b a a a b a a

结束，最小子串长度为4，即abaa 。

接着统计了下二进制字符长度（X轴）和周期性字符串个数/概率（Y轴）关系。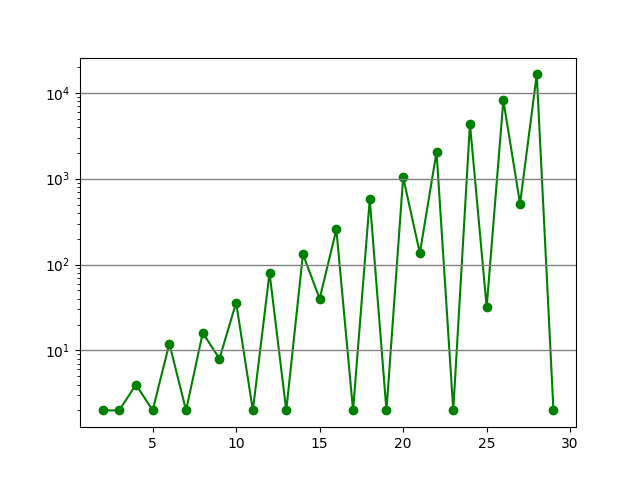

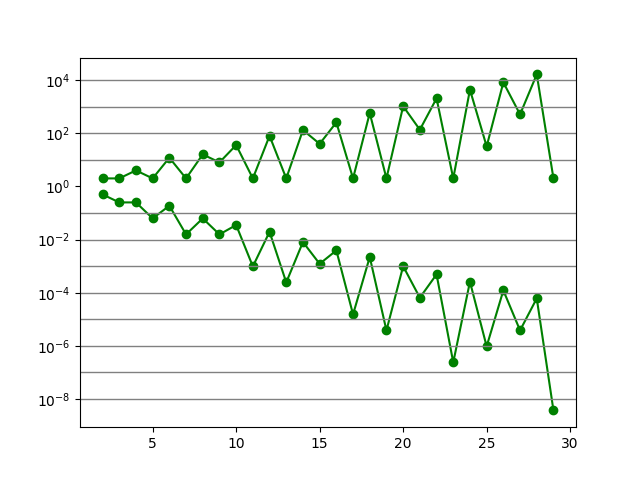
可见，自循环字符串个数和概率与其字符串长度有关，总的来说：

1. 长度越长，包含的自循环的字符串个数越多，呈指数增加
2. 长度越长，字符串可能是自循环的概率降低，呈指数下降
3. 素数只有两个自循环字符串（全0，全1）
4. 包含分解因子越多，越可能包含更多自循环字符串