核心思想
将矩阵A 以单位矩阵作为陪矩阵 [A | I]。通过同时变换矩阵A 和单位矩阵I ,使得A 变为单位矩阵,I 经过得到相应的变换得到的矩阵就是矩阵A 的逆矩阵A-1。
例子
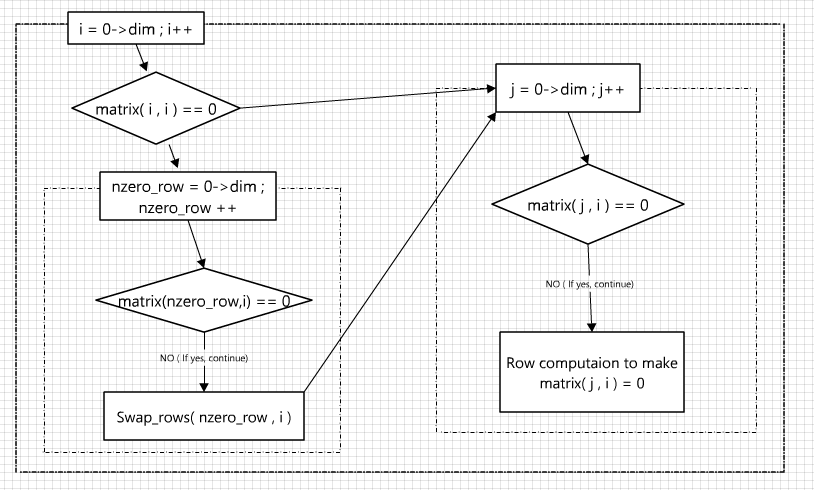
流程
代码
1: Matrix8g Inverse( Matrix8g &mat){
2: Matrix8g mat_inv;
3: Matrix8g mat_cpy;
4: int dim;
5: int i, nzero_row,j;
6: uint8_t temp, jtimes;
7:
8: assert(mat.rr == mat.cc);
9: dim = mat.rr;
10: /* mat_cpy = mat;*/
11: Copy(mat_cpy , mat);
12:
13: mat_inv.Make_identity(mat.rr, mat.cc);
14:
15: /* from column 0 to column dim-1;
16: * dim = this.rr = this.cc */
17: for(i = 0; i < dim; i++){
18: nzero_row = i;
19: /* matrix(i, i) == 1 add the nzero_row th row
20: * which elems[nzero_row*dim +i] != 0 to the ith row*/
21: if(mat_cpy.Get(i,i) == 0){
22: do{
23: ++nzero_row;
24: if(nzero_row >= dim)
25: ERROR("Non-full rank matrix!");
26: temp = mat_cpy.Get(nzero_row,i);
27: }while((temp == 0)&&(nzero_row < dim));
28: mat_cpy.Swap_rows(i,nzero_row);
29: mat_inv.Swap_rows(i,nzero_row);
30: }
31: /* matrix(i, i) != 0 now */
32: for(j = 0; j < dim; j++){
33: /* if matrix(j,i) == 0; then */
34: if(mat_cpy.Get(j,i) == 0)
35: continue;
36: if(j != i){
37: jtimes = (uint8_t)galois_single_divide(mat_cpy.Get(j,i), mat_cpy.Get(i,i), 8);
38: mat_cpy.Row_plus_irow(j, i, jtimes);
39: mat_inv.Row_plus_irow(j, i, jtimes);
40: }
41: else{
42: jtimes = (uint8_t)galois_inverse(mat_cpy.Get(i, i), 8);
43: mat_cpy.Row_to_irow(i , jtimes);
44: mat_inv.Row_to_irow(i , jtimes);
45: }
46:
47: }
48: }
49: return mat_inv;
50: }
同样的另一篇关于Guass – Jardon 消元计算逆矩阵:http://www.codelast.com/?p=1288



这个代码是自己编程实现的,还是网上下载的呢?:)
自己写的