本文讨论分布式存储系统如果采用编码方式保存数据，那么允许最多失效的节点个数与码率之间的关系。这个关系也可以通过图论中“最小分割最大流”定理来求证。

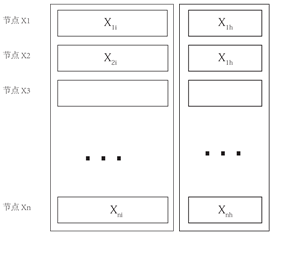
一个原始文件S（假设没有冗余信息）大小自信息量/文件大小为I ，进行冗余编码[n’,k]（这里考虑系统码，为和分不到n 个节点区分开，用n’ 代替）的编码率为R = k/n’ ，则编码后文件大小为C：I → C = I/R。将编码后的数据分布在n 个节点上，每个节点的数据记做：X1 ，X2 ，X3 ……Xn ，每个节点数据的大小为C/n = I/R·n 。而每个节点数据/信息又有两部分组成，前一部分是系统码中的原始信息：X_ii = I/n，另一部分是系统码中的校验信息：X_ih = C/n – I/n ，且X_i = X_ii + X_ih。如下图所示

当a 个节点发生故障失效时，那么剩下的校验/冗余信息和原始信息应该能够恢复出丢失的原始信息，进而恢复出所有的校验信息。即：

  因为H = C – I =I/R – I。得结果：

这也就是说，所有没有损坏节点的个数与所有节点比率（n-a/n）应该大于编码码率R。