日度归档：2012/05/22

Cuckoo Hash 布谷鸟哈希

Posted on by
2

布谷鸟哈希最早于2001 年由Rasmus Pagh 和Flemming Friche Rodler 提出。该哈希方法是为了解决哈希冲突的问题而提出，利用较少计算换取了较大空间。名称源于该哈希方法行为类似于布谷鸟在别的鸟巢中下蛋，并将别的鸟蛋挤出的行为。它具有占用空间小、查询迅速等特性，可用于Bloom filter 和内存管理。

算法描述

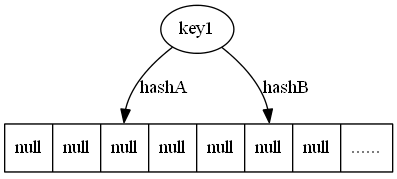
算法使用hashA 和hashB 计算对应key 的位置。

  1. 当两个哈希任意位置为空，则选择一个位置插入
  2. 让两个哈希有位置为空时，则插入到空位置
  3. 当两个哈希位置均不为空时，随机选择两者之一的位置上keyx 踢出，计算踢出的keyx 另一个哈希值对应的位置进行插入，转至2执行（即当再次插入位置为空时插入，仍旧不为空时，踢出这个keyy）

图例

1. 插入key1 两个位置均为空,则插入任意位置.

1

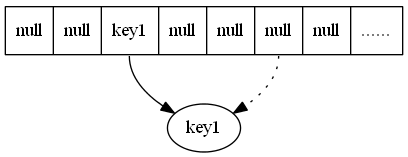
2. 插入后

2

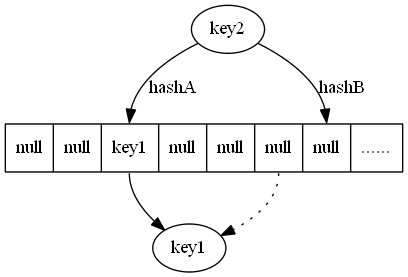
3. 插入key2 两个位置有一个位置为空,则插入空的位置中

3

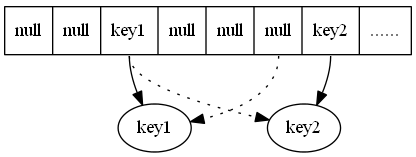
4. 插入后效果

4

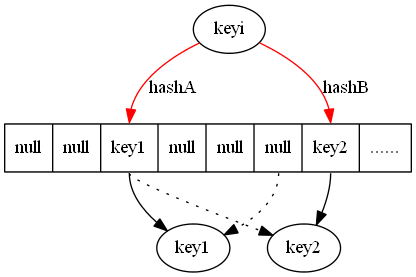
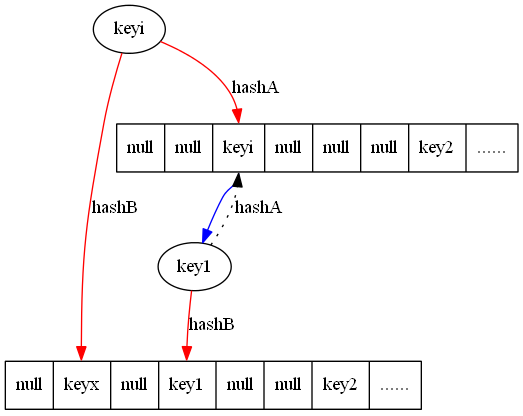
5. 新插入keyi 发现对应两个位置均被占据

 

5

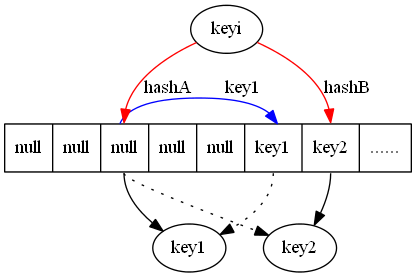
6. 随机选择一个位置提出所在位置的key（key1），将踢出的key 放置在另一个哈希结果对应的位置上

6

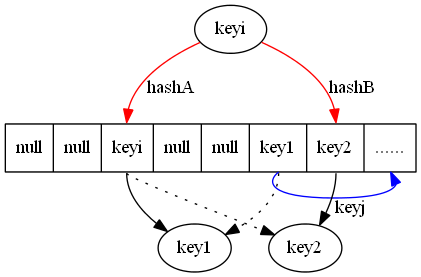
7. 如果踢出的key（key1）又占据/踢出了其他key（keyj）的位置，则反复执行上面的过程直到结束

7

其他

  1. Cockoo hash 有两种变形。一种通过增加哈希函数进一步提高空间利用率；另一种是增加哈希表，每个哈希函数对应一个哈希表，每次选择多个张表中空余位置进行放置。三个哈希表可以达到80% 的空间利用率。
  2. Cockoo hash 的过程可能因为反复踢出无限循环下去，这时候就需要进行一次循环踢出的限制，超过限制则认为需要添加新的哈希函数。
  3. 在SOSP 11 的SLIT 文章中有使用Cockoo hash。

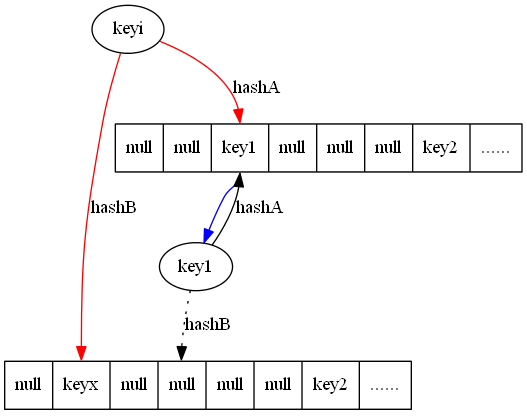
增加哈希表过程如下：

当新插入一个key hashA 在上面哈希表位置和hashB 在下面哈希表的位置分别被key1 和keyx 占据，任选一个key 提出（这里选择key1）。

11

计算key1 hashB 的值然后插入到下面的hashB 对应的哈希表中。

 

12

PS

文中图使用graphviz 绘制，图例第七张图片生成文件如下：

   1: digraph G {

   2: "node0" [

   3: label = "<f0>null | <f1>null | <f2>keyi | <f3>null | <f4>null | <f5>key1 | <f6>key2 | <f7>......"

   4: shape = "record"

   5: ];

   6: 

   7: "node2"[

   8: label="key1"

   9: ];

  10: 

  11: "node3"[

  12: label="key2"

  13: ];

  14: 

  15: "node1"[

  16: label="keyi"

  17: ];

  18: 

  19: "node1"->"node0":f2[color="red",shape="record",label="hashA"];

  20: "node1"->;"node0":f6[color="red",shape="record",label="hashB"];

  21:  

  22: "node0":f2->;"node2";

  23: "node0":f5->;"node2"[style="dotted"];

  24:  

  25: "node0":f2->;"node3"[style="dotted"];

  26: "node0":f6->;"node3";

  27:  

  28: "node0":f5:s->;"node0":f7:s[color="blue",shape="record",label="keyj"];

  29: }

在GVEdit 在使用的时候，F5 是生成图片，并在对应的目下生成了响应的图形文件，相关设置在Graph setting 里面，第一次用的时候总是找不到export image 的方法，总导出不了对应图片。

纠删码（erasure correct code）下的块可用概率

Posted on by
1

假设：

  1. 一个系统中有N 台机器，M 台为当前故障机器
  2. 使用的纠缠码保证每个块被划分为n 个分片，每个机最多保存一个分片
  3. 需要恢复一个分片最少需要m 个分片

那么一个块在当前可用性概率为：

$P_0 = \sum^{n-m}_{i=0}\frac{\binom{M}{i}\binom{N-M}{n-i}}{\binom{N}{n}}$

  • $P_0$ 是一个块可用的概率
  • n 是所有分片的数目
  • m 为恢复块所需分片的最少数目
  • N 是所有可保存分片的机器
  • M 是当前不可用的机器

说明：

根据全概率公式（某个事件的概率，是该事件在所有情况下的概率的总和）

$\Omega = \sum^{n}_{k=1}A_k P(B)=\sum^{n}_{k=1}P(A_k)P(B|A_k)$

$\Omega = \sum^{n}_{k=1}A_k $是对B 的一个空间全划分，即包含了B 所有情况。这里的划分是将所有故障机器可能包含的分片（从0 到 n-m，如果超过n-m，那么可用的机器保存的分片少于m 个，也就无法恢复该块数据）。每一个$P_x=\frac{\binom{M}{i}\binom{N-M}{n-i}}{\binom{N}{n}}$ 都代表着：当M 个故障机器中有i 个分片情况下，该事件（块可以被恢复）在所有可能情况下的概率。

既然$\Omega = \sum^{n}_{k=1}A_k $可以是对所有故障机器可能包含分片的划分，也就可以是对所有正常机器可能包含的分片有：

$P_0 = \sum^{n}_{i=m}\frac{\binom{N-M}{i}\binom{M}{n-i}}{\binom{N}{n}}$

即概率等于将i 个可用分片放置到N-M 个可用机器乘以将n-i 个分片放置到M 个故障机器上，除以将全部n 个分片放置到所有N 个机器上的概率。

实例：

举例：n=4，m=2，N=5，M=2 。很容易知道，这个块可用的概率为1 。根据公式

$P_0 = \sum^{2}_{i=0}\frac{\binom{2}{i}\binom{3}{4-i}}{\binom{5}{4}}=\frac{(C^{1}_{2}C^{3}_{3}+C^{2}_{2}C^{2}_{3})}{5}=1$

其中有当i=0 时排除该一项，因为三个节点不可能保存四个分片。

根据另外一个公式可以得到同样结果。