假设：

一个系统中有N 台机器，M 台为当前故障机器
使用的纠缠码保证每个块被划分为n 个分片，每个机最多保存一个分片
需要恢复一个分片最少需要m 个分片

那么一个块在当前可用性概率为：

$P_0 = \sum^{n-m}_{i=0}\frac{\binom{M}{i}\binom{N-M}{n-i}}{\binom{N}{n}}$

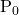$P_0$ 是一个块可用的概率
n 是所有分片的数目
m 为恢复块所需分片的最少数目
N 是所有可保存分片的机器
M 是当前不可用的机器

说明：

根据全概率公式（某个事件的概率，是该事件在所有情况下的概率的总和）

$\Omega = \sum^{n}_{k=1}A_k P(B)=\sum^{n}_{k=1}P(A_k)P(B|A_k)$

$\Omega = \sum^{n}_{k=1}A_k$ 是对B 的一个空间全划分，即包含了B 所有情况。这里的划分是将所有故障机器可能包含的分片（从0 到 n-m，如果超过n-m，那么可用的机器保存的分片少于m 个，也就无法恢复该块数据）。每一个 $P_x=\frac{\binom{M}{i}\binom{N-M}{n-i}}{\binom{N}{n}}$ 都代表着：当M 个故障机器中有i 个分片情况下，该事件（块可以被恢复）在所有可能情况下的概率。

既然 $\Omega = \sum^{n}_{k=1}A_k$ 可以是对所有故障机器可能包含分片的划分，也就可以是对所有正常机器可能包含的分片有：

$P_0 = \sum^{n}_{i=m}\frac{\binom{N-M}{i}\binom{M}{n-i}}{\binom{N}{n}}$

即概率等于将i 个可用分片放置到N-M 个可用机器乘以将n-i 个分片放置到M 个故障机器上，除以将全部n 个分片放置到所有N 个机器上的概率。

实例：

举例：n=4，m=2，N=5，M=2 。很容易知道，这个块可用的概率为1 。根据公式

$P_0 = \sum^{2}_{i=0}\frac{\binom{2}{i}\binom{3}{4-i}}{\binom{5}{4}}=\frac{(C^{1}_{2}C^{3}_{3}+C^{2}_{2}C^{2}_{3})}{5}=1$

其中有当i=0 时排除该一项，因为三个节点不可能保存四个分片。

根据另外一个公式可以得到同样结果。

呆鸥

Brains first and then Hard Work

纠删码（erasure correct code）下的块可用概率

假设：

那么一个块在当前可用性概率为：

说明：

实例：

《纠删码（erasure correct code）下的块可用概率》上有1条评论

发表回复取消回复

假设：

那么一个块在当前可用性概率为：

说明：

实例：

《纠删码（erasure correct code）下的块可用概率》上有1条评论

发表回复 取消回复

发表回复取消回复