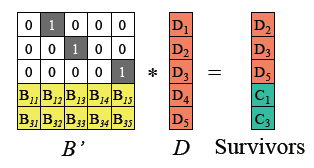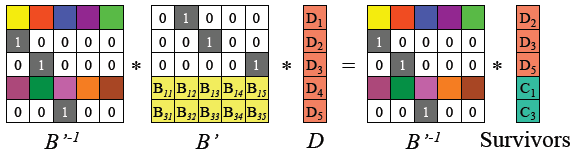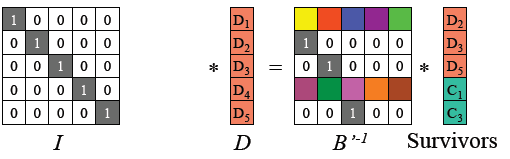最近获悉facebook 在hadoop 中使用纠删码,节约存储成本。纠删码相比副本具有更高的存储效率(k/n>1/n)。缺点是计算量大,重建复杂。RAID5 、RAID6 就是纠删码的最简单应用。下面使用图解的方式介绍纠删码的基本原理。
-
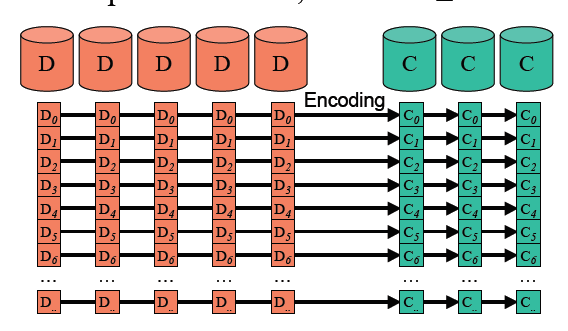
下图给出纠删码在物理逻辑层次应用的一个场景: D 是Data Device ,用于保存数据,C 是校验位,用于重建恢复数据,C 是D 通过纠删码编码得到的,如最常见的纠删码Reed-Solomen 码。
-
每个条带上的数据块生成对应条带上的校验块,数据块大小和校验块大小相同,一般把数据块的个数用k 表示,n 表示数据块和校验块总数,这样的编码称为[k,n] 编码,最多可以容n-k 个Data Devices 失效。
-
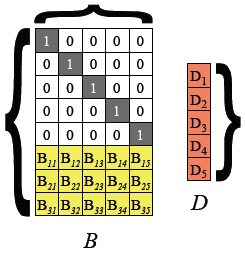
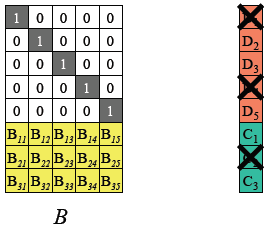
如下图,假设一个条带上的数据块用矩阵D 表示,生成数据块D 的校验矩阵需要矩阵B 的帮助,如下图所示,B 由两部分组成上面是一个k×k 大小的单位矩阵I ,下面是生成校验位的n-k×k 大小的矩阵B*。
-
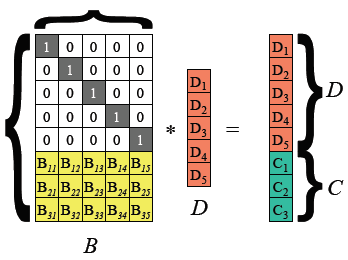
这两部分分别与数据矩阵D 相乘生成两部分分别为数据部分D 和校验部分C(如下所示)。
-
这两部分分别是由 I×D 和 B–×D 所生成的。
-
如果数据中的数据块或者校验块发生了丢失,需要出原始的数据块。
-
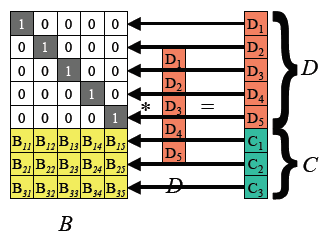
去掉丢失的数据块校验块对应在矩阵B 的行(row),得到矩阵B’ ,那么满足下面的等式:
-
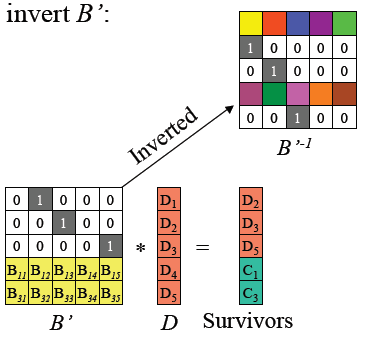
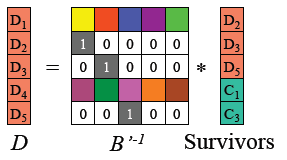
对B’ 求逆矩阵得到B’-1 ,且我们知道矩阵B’ 和原始数据矩阵D 之积为去掉损坏数据的矩阵Survivours,满足下面的等式。
-
为了求得原始数据,在上面等式两边左侧乘以B’ 的逆
-
矩阵B’-1 和B’ 之积为k×k 的单位矩阵
-
那么等式左侧即为原始数据。这样通过剩余数据矩阵Survivors 乘以对应矩阵B 的系数组成的矩阵的逆,就得到了数据矩阵,最终得到了原始数据。有了原始数据,校验数据也就不难求了。
文中图来源于这里
上面图解还存在两个问题就是B’ 是否存在逆矩阵,如果rank(B’)<k,那么B’ 就不存在逆矩阵了,另外一个问题就是矩阵B 除掉上面单位矩阵I 后的矩阵B* 是如何生成的?
这两个问题可以一起回答,答案是范德蒙矩阵,范德蒙矩阵B 满足任意k 行(row)线性不相关(len(col)>=len(row)),范德蒙矩阵B可以通过列变换为系统码的生成矩阵,即前k行k列形成一个单位矩阵。但如果B 是范德蒙矩阵就不到系统码(编码过后码字中存在原始数据称为系统码),那么对B 进行个处理,将n×k 大小的范德蒙矩阵分为上面k×k 大小的矩阵B1 和下面n-k×k 大小的矩阵B2,通过右乘以B1 矩阵的逆得到[[B1]|[B2]]-T × [B1]-1 = [[B1]·[B1]-1 |[B2]·[B1]-1 ]-T = [ I |[B2]·[B1]-1 ]-T 。B* = [B2]·[B1]-1