B- 树和B+-树是重要的两个用于数据检索的数据结构,广泛用在文件系统、数据库和数据检索中。
【重申】没有“B’减’树”这样的树,在之前的’-‘ 是个横杠杠
B- 树
类似于二分查找树。但不同于二分查找树,B 树可以有多个孩子节点,这样树的深度就不会太深,其次B 树是平衡树,即所有叶子节点到根节点路径长度一样,所有非叶子节点的孩子节点都满足一定条件(不少于![]() 、不多于m,m 为阶数),这样查找一个节点就不会便利太深。对B 树有这样的限制:
、不多于m,m 为阶数),这样查找一个节点就不会便利太深。对B 树有这样的限制:
- 非叶子节点有至少
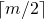 个、至多m 个子节点
个、至多m 个子节点 - 根节点可以至少有两个节点
- 所有叶子节点在同一层
- 有k 个子节点的非根节点恰好包含k-1 个关键码(key)
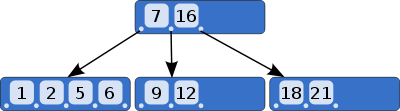
满足上面四个要求的树就是B 树。下图是一个m=5阶B 树例子,每个节点最少![]() 个、最多5 个节点(指针)。关键码是用于区分左右子树(左边子树关键码都比该节点小,右边子树关键码都比该节点大),且非叶子节点和叶子节点关键码内都包含了关键码对应的数据信息(这点和B+ 树不同)。当插入和删除时会发生树的合并和拆分,具体参考【B树 和B+ 树】【性能分析】【动态动画演示】。
个、最多5 个节点(指针)。关键码是用于区分左右子树(左边子树关键码都比该节点小,右边子树关键码都比该节点大),且非叶子节点和叶子节点关键码内都包含了关键码对应的数据信息(这点和B+ 树不同)。当插入和删除时会发生树的合并和拆分,具体参考【B树 和B+ 树】【性能分析】【动态动画演示】。
B 树内没有重复的关键码,且把关键码相近的放在一起,利用了访问的局部性原理。根据第一点B 树有一定比率的非叶子节点是满的(>50%,B* 树可保证>75%),这样就能够提高空间利用率,减少检索和更新磁盘读取次数。但B- 树也有自己的问题:
- 因为非叶子节点上的关键码也包含了对应的信息,所以非叶子节点也会变得比较大,影响了阶数m 的扩展
- 当需要获取全部或者某个区段的关键码对应的信息,需要遍历B 树
B+-树
B+ 树针对B 树一些性能上的缺陷进行了改进,所以B+ 树在使用上更加广泛,通过性能分析和实际应用发现B+ 树比B 树更优。B+ 结构是这样定义的:
- 每个节点(除了根节点)至少有
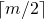 个、至多m 个子节点(同B 树)
个、至多m 个子节点(同B 树) - 根节点至少有两个子节点
- 有k 个子节点的节点必有k 个关键码
- 每个叶子节点都有指向下一个叶子节点的指针
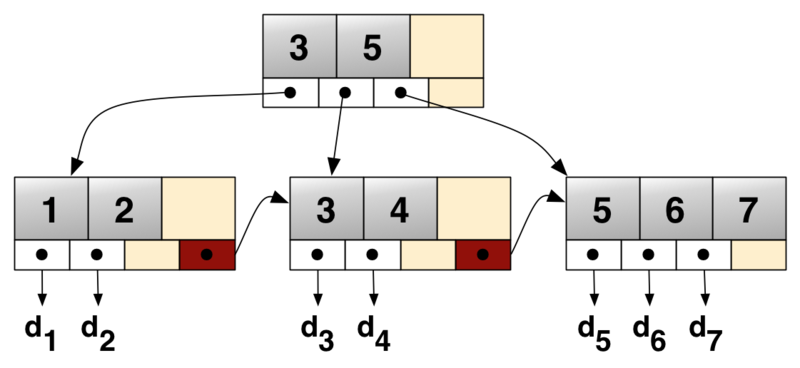
从结构上看B+ 树减少了一个指向叶子节点的指针,B 树中关键码是左右子树的划分,不与子节点的某个关键码相同,而在B+ 树中关键码可以与右子树最小的关键码相同,这是因为B+ 树中只有非叶子节点才真正保存关键码对应的信息,而非叶子节点只是用来划分叶子节点和保存叶子节点关键码索引而已。这样非叶子节点就变得非常简单阶数m 也可以取得比较大(类似于文件系统中的inode,如果inode 中也保存了一些数据块的话就会变得很大,每次访问inode 就变得慢了)。
第二个变化就是如下图在每个叶子节点上都有连接下一个叶子节点的指针,这样就将所有的叶子节点以线性检索链表的方式连接了起来。在范围查询和做检查点或者备份时会更快。
如果你觉得讲的太简单了,可以参考这里,没见过比那讲的更详细的了!但我个人感觉自己理解了就OK 了,总不至于要自己去写一个B 树的算法~