参考 The Byzantine Generals Problems 。
这个问题的最初描述是:n 个将军被分隔在不同的地方,忠诚的将军希望通过某种协议达成某个命令的一致(比如一起进攻或者一起后退)。但其中一些背叛的将军会通过发送错误的消息阻挠忠诚的将军达成命令上的一致。Lamport 证明了在将军总数大于3m ,背叛者为m 或者更少时,忠诚的将军可以达成命令上的一致。
为了保证上面的需求,必须满足下面两个条件:
1. 每两个忠诚的将军必须收到相同的值 v(i)(v(i)是第i 个将军的命令)
2. 如果第i 个将军是忠诚的,那么他发送的命令和每个忠诚将军收到的v(i)相同
为了简化以上模型,我们使用一个将军发送命令给多个副官的形式来证明,发送命令的将军称为发令者,接收命令的将军为副官,那么上面的两个条件可以表述为:
IC1. 所有忠诚的副官遵守相同的命令
IC2. 如果发出命令的将军是忠诚的,那么所有忠诚的副官遵守相同的命令
特别提示:发送命令的每次只有一个将军,将其命令发送给n-1 个副官。m 代表叛国者的个数,因为将军总数为n,所以副官总数为n-1 个。IC2 中副官遵守实际上是指忠诚的将军能够正确收到忠诚将军的命令消息。
一、通过口头消息
通过口头消息传递达到一致,如果有m 个叛国将军,则将军们的总数必须为3m+1 个以上。下面是口头消息传递过程中默认的一些条件:
A1. 每个被发送的消息都能够被正确的投递
A2. 信息接收者知道是谁发送的消息
A3. 能够知道缺少的消息
A1 和A2 假设了两个将军之间通信没有干扰,既不会有背叛者阻碍消息的发送(截断)也不会有背叛者伪造消息的情况(伪造)。即是每个将军都可以无误地将自己的消息发送给其他每个将军。(下一节中可以不需要这个必要条件)
我们定义口头消息算法OM(m) 。对于所有的非负整数m ,每个发令者通过OM(M) 算法发送命令给n-1 个副官。下面将说明OM(m) 算法在最多有m 个背叛者且总将军数为3m+1 或者更多的情况下可以解决拜占庭将军问题。(考虑到网络应用实际环境,原文使用了收到值代替收到命令,本文不做修改)
算法定义一个函数:![]() 等于多数派命令。
等于多数派命令。
OM(0)算法
(1)发令者将他的命令发送给每个副官。
(2)每个副官采用他从发令者发来的命令,或者默认使用撤退命令,如果没有收到任何命令。
OM(m)算法
(1)发令者将他的命令发送给每个副官。
(2)对于每个i ,vi 是每个副官i 从发令者收到的命令,如果没有收到命令则为撤退命令。副官i 在OM(m-1) 中作为发令者将vi 发送给另外n-2 个副官。
(3)对于每个i,并且![]() ,vj 是副官i 从第(2)步中的副官j 发送过来的命令(使用OM(m-1) 算法),如果没有收到第(2)步中的副官j 的命令则默认为撤退命令。最后副官i 使用
,vj 是副官i 从第(2)步中的副官j 发送过来的命令(使用OM(m-1) 算法),如果没有收到第(2)步中的副官j 的命令则默认为撤退命令。最后副官i 使用![]() 得到命令。
得到命令。
接下来实际的考虑一个n=4,m=1 的情况:
1. 当副官3 是背叛者,以副官2 为例
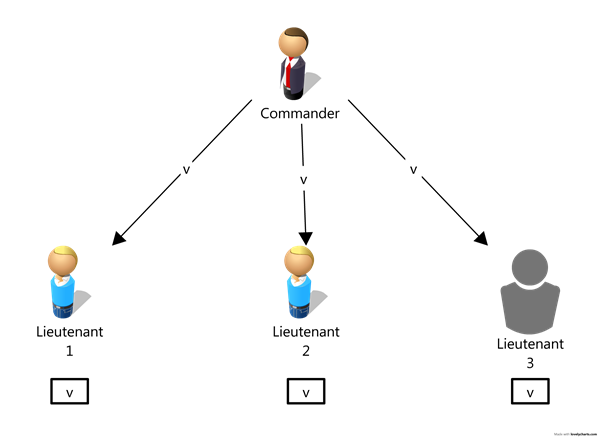
第一步发令者执行算法OM(1)将自己的命令发送给三个副官,三个副官都正确地收到了命令。
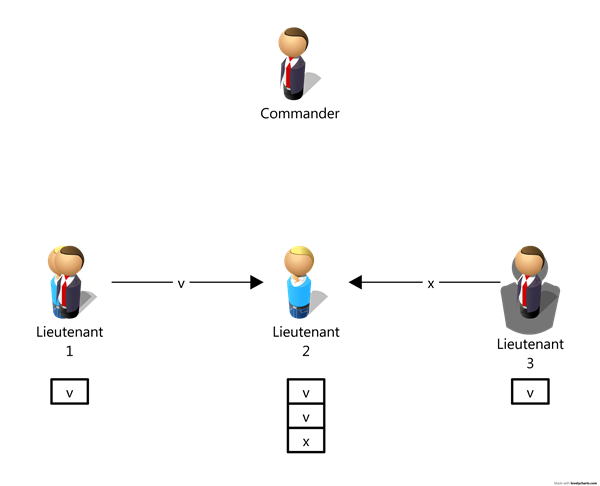
第二步每个收到命令的副官都作为发令者执行算法OM(0),将自己的命令转发给其余副官,因为副官3是背叛者,所以他给副官2 传递的消息会是假消息。副官2 最后根据majority 函数来决定命令。
这样背叛的副官3 同理也干扰不了忠诚的副官1 和发令者的决定。下面看看如果发令者是背叛者。
2. 发令者是背叛者,其余副官为忠诚的
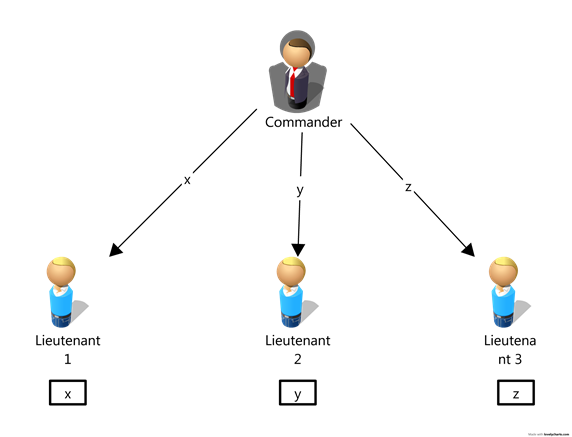
第一步:发令者向副官发送了不同的命令,实际情况中是一个攻击者向不同方发送了不同的值进行欺骗。
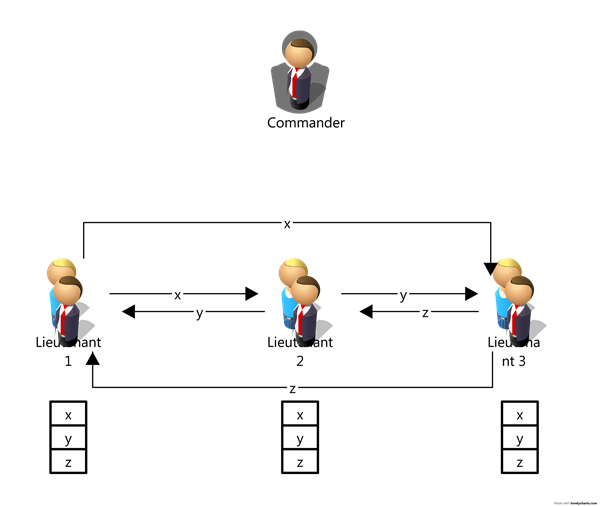
第二步:副官收到命令后,摇身一变为发令者执行OM(0) 向所有的副官发送命令,这样所有副官的到命令会都相同(<x,y,z>),这样所有命令都达不到大部分。
文章接着就证明了OM(m) 算法对任意m 都是可以满足,首先引入一个引理(归纳法证明):
引理1:对于任意m 和k ,如果有超过2k+m 个将军和最多k 个背叛者,那么算法OM(m) 满足IC2 (回顾下IC2 指的是,如果将军是忠诚的,所有的副官遵守将军命令)。
证明:当m=0 的时候,OM(0) 在将军是忠诚的时候满足IC2。当m>0 时,首先将军将命令传递给 n-1 个副官,然后每个副官对n-1 个将军执行OM(m-1) 算法。因为假设了n>2k+m(引理中有将军数大于2k+m),所以 ![]() (即每一轮中副官总数不小于背叛者的两倍),这样每轮OM(m-k) 算法中忠诚的副官收到的命令都是
(即每一轮中副官总数不小于背叛者的两倍),这样每轮OM(m-k) 算法中忠诚的副官收到的命令都是![]() ,其中忠诚副官发送的命令大于或者等于一半。
,其中忠诚副官发送的命令大于或者等于一半。![]()
接着解决拜占庭将军问题。
定理1:对于任意m,如果有超过3m 个将军和最多m 个背叛者,算法OM(m) 满足条件IC1 和条件IC2。
证明:通过m 的归纳法证明,我们通过假设OM(m-1) 成立来证明OM(m) m>0。首先考虑发送命令的将军是忠诚的。那么将引理中k 设为m 则OM(m) 满足IC2 ,IC1 在发令将军是忠诚的情况下也满足。
接着考虑m 个背叛者中有一个是发令者,那最多就只有m-1 个副官是背叛者了,又因为有3m 个将军,所以副官的总数超过3m-1,且有3m-1>3(m-1) 。因此通过归纳法假设 OM(m-1) 满足IC1 和IC2(最多3(m-1) 个将军和最多m-1 个背叛者)。那么任意两个忠诚的副官j 在OM(m-1) 获得相同命令![]() ,那么在OM(m) 算法中每个忠诚的副官都会收到
,那么在OM(m) 算法中每个忠诚的副官都会收到 ![]() ,可知满足条件IC1 和IC2。
,可知满足条件IC1 和IC2。![]()
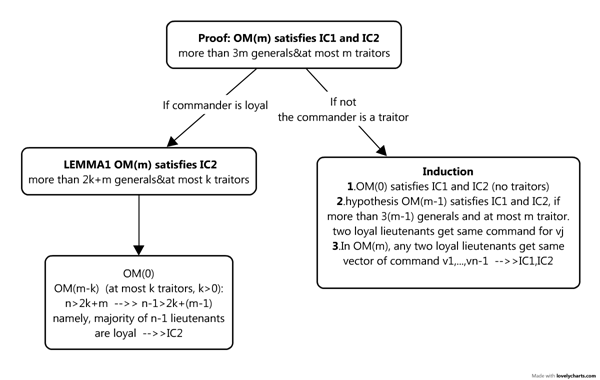
看完这段证明其实我也挺糊涂的~~~~,画了张图来看看lamport 是怎么证明的:
二、通过签名消息
签名消息在除了满足口头消息A1-A3 三点要求外还应该满足下面A4:
A4 (a)签名不可被伪造,一旦被篡改即可发现
(b)任何人都可以验证将军签名的可靠性
下面定义一个类似于上面majority() 函数的choice() 来决定副官的选择:1.当集合V 只包含了一个元素v ,那么choice(V)=v ;2. choice(![]() )=RETREAT。
)=RETREAT。
有了上面A4 和choice() 基础我们给出SM(m) 方法:
SM(m) 算法
初始化![]()
(1)将军签署命令并发给每个副官
(2)对于每个副官i :
(A)如果副官i 从发令者收到v:0 的消息,且还没有收到其他命令序列,那么:
(i)使![]() 为{v}
为{v}
(ii)发送v:0:i 给其他所有副官
(B)如果副官i 收到消息![]() 且v 不在集合
且v 不在集合![]() 中则
中则
(i)添加v 到![]()
(ii)如果k<m ,那么发送![]() 给每个不在
给每个不在![]() 中的副官
中的副官
(3)对于每个副官i ,当不再收到消息,则遵守命令choive(![]() )
)
算法的几点说明:
- 算法第三步并没有说明副官如何判断没有新的消息,可以通过两个解决方法:一是要求每个副官收到消息后要么签名转发该消息,要么发送一个通知他将不发送这个消息;二是设置一个超时时间,如果在该时间段还没有收到消息,则认为不再收到消息。
- 算法SM(m) 中,让副官签名是确认其收到了该消息(有点像来了份文件给每个领导批阅)。在SM(1) 中副官收到消息就不用签字了,因为不用转发给其他副官。
定理2:对于任意m,最多只有m 个背叛者情况下,算法SM(m) 解决拜占庭将军问题
Proof:首先证明IC2,如果发令者是忠诚的,那么所有的副官一定收到相同的命令,因为签名无法篡改,且IC1 也就满足了。证明IC1 只用考虑发令者是背叛者的情况(重新回顾下IC1 是指所有忠诚的副官执行相同的命令),IC1 要求两个忠诚的副官(i,j)必须收到相同的命令集合![]() 、
、![]() ,也就是
,也就是![]() 中每个v 都在
中每个v 都在![]() 中。会存在两种情况,其一当副官i 收到v 命令的序列后,加入到
中。会存在两种情况,其一当副官i 收到v 命令的序列后,加入到![]() ,并将其发送给副官j ,j 将命令v 保存;其二副官i 收到命令
,并将其发送给副官j ,j 将命令v 保存;其二副官i 收到命令![]() ,其中有
,其中有![]() =j,所以 由A4 可知副官j 也收到了该命令。如果没有,则有:
=j,所以 由A4 可知副官j 也收到了该命令。如果没有,则有:
- k<m。这种情况下,i 发送信息
 给副官j ,那么j 一定收到v 。(这点感觉和上面有重复)
给副官j ,那么j 一定收到v 。(这点感觉和上面有重复) - k=m。发令者是背叛者,最多只有m-1 个副官是背叛者。因此,最少有一个序列
 是忠诚的。那么j 一定收到这个忠诚的副官序列发来的值v ,所以副官j 收到v 。
是忠诚的。那么j 一定收到这个忠诚的副官序列发来的值v ,所以副官j 收到v 。
证明完毕。![]()
后面讨论的是如果消息丢失和超时等系统稳定性的,这里就不做介绍了。