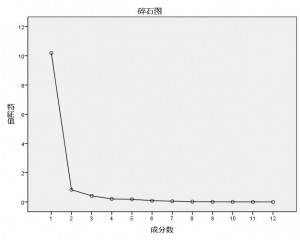
因子分析是模式识别中降维的一个重要方法,它把具有相关性的多个特征参数去相关性,提取出因子进行分析,有效的减少了计算量,但通过 SPSS 实验发现,如果进行因子分析后,得到的因子对分类的贡献值不相同,通过碎石图可以看到少量因子对聚类贡献大,更多的因子对聚类贡献小,如果把它们同等对待进行下一步的聚类(如 k-means 聚类)会严重影响聚类结果,导致还不如用一个因子进行聚类。下面是计算因子的方法:
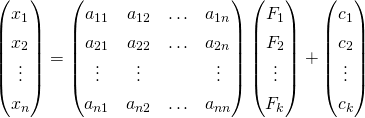
![]()
X 为可实测的 n 维随机向量,它的每个分量代表一个指标或者变量。F 为不可观测的 K 维随机向量,它的各个分量将出现在每个变量中,所以称它们为公共因子,矩阵 A 称为因子载荷矩阵,![]() 为载荷因子,变量 c 称为随机因子,包括随机误差。值得注意的是 F 中每个分量的公共因子的重要程度可以通过碎石图看到(越重要,值越大,对聚类影响更大):
为载荷因子,变量 c 称为随机因子,包括随机误差。值得注意的是 F 中每个分量的公共因子的重要程度可以通过碎石图看到(越重要,值越大,对聚类影响更大):